题目内容
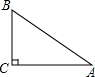
如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边，△ABC最小的角为A，求tanA的值．
∵x2-4x+3=0
∴（x-1）（x-3）=0，
解得：x1=1，x2=3，
∵方程x2-4x+3=0的两个根分别是Rt△ABC的两条边，△ABC最小的角为A，
当BC=1，AC=3，
∴tanA的值为：
=
，
当BC=1，BC=3，
∴AC=2
，
∴tanA的值为：
=
=
．
∴tanA的值为：
或
．
∴（x-1）（x-3）=0，
解得：x1=1，x2=3，
∵方程x2-4x+3=0的两个根分别是Rt△ABC的两条边，△ABC最小的角为A，
当BC=1，AC=3，
∴tanA的值为：
| BC |
| AC |
| 1 |
| 3 |
当BC=1，BC=3，
∴AC=2
| 2 |
∴tanA的值为：
| BC |
| AC |
| 1 | ||
2
|
| ||
| 4 |
∴tanA的值为：
| 1 |
| 3 |
| ||
| 4 |
练习册系列答案
阅读快车系列答案
相关题目