题目内容
【题目】手工课上,老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形,聪明的你请在下列四个正方形中画出不同的剪裁线,并直接写出每种不同分割后得到的最小等腰直角三角形面积(注:不同的分法,面积可以相等)
【答案】答案见试题解析.
【解析】
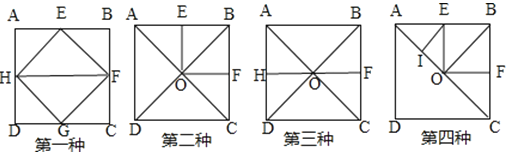
试题分析:(1)正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,连接HE、EF、FG、GH、HF,即可把正方形纸片恰好剪成六个等腰直角三角形;然后根据三角形的面积公式,求出分割后得到的最小等腰直角三角形面积即可;
(2)正方形ABCD中,E、F分别是AB、BC的中点,O是AC、BD的交点,连接OE、OF,即可把正方形纸片恰好剪成六个等腰直角三角形;然后根据三角形的面积公式,求出分割后得到的最小等腰直角三角形面积即可;
(3)正方形ABCD中,F、H分别是BC、DA的中点,O是AC、BD的交点,连接HF,即可把正方形纸片恰好剪成六个等腰直角三角形;然后根据三角形的面积公式,求出分割后得到的最小等腰直角三角形面积即可;
(4)正方形ABCD中,E、F分别是AB、BC的中点,O是AC的中点,I是AO的中点,连接OE、OB、OF,即可把正方形纸片恰好剪成六个等腰直角三角形;然后根据三角形的面积公式,求出分割后得到的最小等腰直角三角形面积即可.
试题解析:根据分析,可得:
 .
.
(1)第一种情况下,分割后得到的最小等腰直角三角形是△AEH、△BEF、△CFG、△DHG,每个最小的等腰直角三角形的面积是:(4÷2)×(4÷2)÷2=2×2÷2=2(cm2);
(2)第二种情况下,分割后得到的最小等腰直角三角形是△AEO、△BEO、△BFO、△CFO,每个最小的等腰直角三角形的面积是:(4÷2)×(4÷2)÷2=2×2÷2=2(cm2);
(3)第三种情况下,分割后得到的最小等腰直角三角形是△AHO、△DHO、△BFO、△CFO,每个最小的等腰直角三角形的面积是:(4÷2)×(4÷2)÷2=2×2÷2=2(cm2);
(4)第四种情况下,分割后得到的最小等腰直角三角形是△AEI、△OEI,每个最小的等腰直角三角形的面积是:(4÷2)×(4÷2)÷2÷2=2×2÷2÷2=1(cm2).