题目内容
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.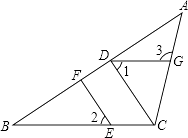
(1)CD与EF平行吗?请说明理由.
(2)如果∠1=∠2,且∠ACB=110°,求∠3的度数.
【答案】
(1)解:结论:CD与EF平行.理由如下:
∵CD⊥AB,EF⊥AB,
∴∠BFE=∠BDC=90°,
∴CD∥EF(同位角相等,两直线平行).
(2)解:∵由(1)结论可知CD∥EF,
∴∠2=∠BCD(两直线平行,同位角相等),
∵∠1=∠2,
∴∠BCD=∠1,
∴DG∥BC(内错角相等,两直线平行),
∴∠3=∠ACB=110°(两直线平行,同位角相等).
【解析】(1)依据垂直于同一条直线的两条直线平行进行判断即可;
(2)首先证明DG∥BC,接下来,再依据平行线的性质进行解答即可.
【考点精析】本题主要考查了平行线的判定与性质和三角形的内角和外角的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.

练习册系列答案
相关题目