题目内容
【题目】在等边△ABC中,
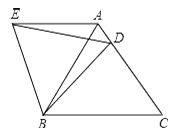
(1)如图1,若D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,求∠BDE的度数;
(2)若点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.请帮助小玉证明CD=BE.
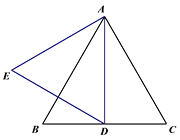
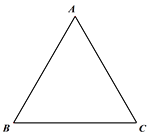
图1 图2
【答案】(1)∠EDB=30°;
(2)作图见解析,证明见解析.
【解析】试题分析:(1)首先根据题目已知条件由等腰三角形三线合一性质可以得出∠ADB=90°,∠BAD=30°,再由AD关于直线AB的对称线段为线段AE可以得出∠EAD=60°,从而可以证明△ADE是等边三角形,继而得出∠ADE=60°,最后计算出∠EDB=30°;(2)要证明CD=BE,我们可以通过证明△EAB≌△DAC证得.
试题解析:
(1)解:∵等边△ABC中, D为线段BC中点,
∴AD⊥BC,AD平分∠BAC,
即∠ADB=90°,∠BAD=30°,
∵AD关于直线AB的对称线段为线段AE,
∴AD=AE,∠EAB=∠BAD=30°,
∴∠EAD=60°,∴△EAD为等边三角形,
∴∠ADE=60°,∴∠EDB=30°;
(2)作图略,
证明:如图,连接AE.

∵AD=DE,∠ADE=60°,
∴△ADE为等边三角形,
∴AE=AD,∠EAD=60°,
∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠EAD =∠BAC,
∴∠EAB=∠DAC,
在△EAB和△DAC中,
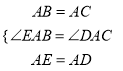 ,
,
∴△EAB≌△DAC,
∴CD=BE.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目