��Ŀ����
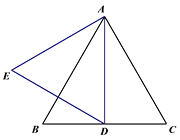
����Ŀ����һ���߳�Ϊm+3�������Σ��Ƚ�������������ڱ߳��ֱ�����1�ͼ���1���õ��ij������������ΪS1.
��1����̽���������ε����S��S1�IJ��Ƿ���һ������������ǣ�������������������ǣ�˵�����ɣ�
��2���ٽ�������������ڱ߳��ֱ�����4�ͼ���2���õ��ij������������ΪS2.
���ԱȽ�S1��S2�Ĵ�С��
����mΪ������ʱ����ij��ͼ�ε��������S1��S2֮�䣨������S1��S2�������Ϊ����������������ֵ����ֻ��16������m��ֵ��
���𰸡���1���⣺S��S1�IJ�����һ��������S��S1�IJ���1;��2������-2m+1��0����-1��m��![]() ʱ��
ʱ��![]() ��
��![]() ����-2m+1��0����m��
����-2m+1��0����m��![]() ʱ��
ʱ��![]() ��
��![]() ����-2m+1= 0����m =
����-2m+1= 0����m =![]() ʱ��
ʱ��![]() =
= ![]() ����m= 9��
����m= 9��
��������
��1��������ȫƽ����ʽ�Ͷ���ʽ���Զ���ʽ�����㼴�ɵõ���.
��2�����ȼ���S1��S2������![]() ���ٷ�������ۣ����ɵõ���.
���ٷ�������ۣ����ɵõ���.
�����������в���ʽ16��![]() ��17�����ɵõ��𰸣�
��17�����ɵõ��𰸣�
��1���⣺S��S1�IJ�����һ��������
��![]() ��
��![]()
��![]() ����S��S1�IJ���1.
����S��S1�IJ���1.
��2����![]()
![]()
��![]() ���൱-2m+1��0����-1��m��
���൱-2m+1��0����-1��m��![]() ʱ��
ʱ��![]() ��
��![]() ��
��
��-2m+1��0����m��![]() ʱ��
ʱ��![]() ��
��![]() ����-2m+1= 0����m =
����-2m+1= 0����m =![]() ʱ��
ʱ��![]() =
= ![]() ��
��
���ɢٵã�S1��S2��-2m+1����![]() ����mΪ����������
����mΪ����������![]() ����һ��ͼ�ε��������S1��S2֮�䣨������S1��S2�������Ϊ����������ֵ����ֻ��16������16��
����һ��ͼ�ε��������S1��S2֮�䣨������S1��S2�������Ϊ����������ֵ����ֻ��16������16��![]() ��17����
��17����![]() ��m��9����m����������m= 9��
��m��9����m����������m= 9��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ���ˮ���̳�ij��̨����ÿ̨���۷ֱ�Ϊ160Ԫ��120Ԫ��A��B�����ͺŵĵ���ȣ��±��ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 4̨ | 1200Ԫ |
�ڶ��� | 5̨ | 6̨ | 1900Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2�����̳����ò�����7500Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�50̨����A���ͺŵĵ��������ܲɹ�����̨��
��3���ڣ�2���������£��̳���������50̨������ܷ�ʵ������1850Ԫ��Ŀ�ꣿ���ܣ��������Ӧ�IJɹ������������ܣ���˵�����ɣ�