题目内容

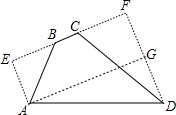
如图，在四边形ABCD中，∠B=135°，∠C=120°，AB=2
3
，BC=4-2
2
，CD=4
2
，则AD边的长为______．
如图，过点A，D分别作AE，DF垂直于直线BC，垂足分别为E，F．
∵∠B=135°，
∴∠ABE=45°，
∴BE=AE=
6
，
∵∠C=120°，
∴∠DCF=60°，
∵CD=4
2
，
∴CF=2
2
，
∴DF=2
6
，
∴EF=4+
6
．
过点A作AG⊥DF，垂足为G．在Rt△ADG中，根据勾股定理得
AD=
(4+
6
)2+(
6
)2
=
(2+
24
)2
=2+2
6
．
故答案为：2+2
6
．
练习册系列答案
相关题目
如图，E在正方形ABCD的边BC延长线上，若CE=AC，AE交D于点F，则∠E=______若AB=2cm，则S△ABE______cm2．
已知在△ABC中，AB=2
3
，AC=2，BC边上的高为
3
，那么BC的长是______．
图（1）是一面矩形彩旗完全展平时（单位：cm），其中矩形ABCD是由白布缝制的穿旗杆用的旗裤，阴影部分CDEF为矫形绸缎旗面．如图（2），将穿好彩旗的旗杆垂直插在操场上，旗杆顶端到地面的高度为220cm．在无风的天气里，求彩旗自然下垂时最低处离地面的高度h．
木工师傅做一个人字形屋梁，如图所示，上弦AB=AC=4m，跨度BC为6m，现有一根长为3m的木料打算做中柱AD（AD是△ABC的中线），请你通过计算说明这根木料的长度是否适合做中柱AD．（只考虑长度、不计损耗）
如图，在线段AE的同侧作正方形ABCD和正方形BEFG（BE＜AB），连接EG并延长交DC于M，过M（1，-1）作MN⊥AB，垂足为N，MN交BD于P．
（1）找出图中一对全等三角形，并加以证明（正方形的对角线分正方形得到的两个三角形除外）；
（2）设正方形ABCD的边长为1，按照题设方法作出的四边形BGMP，若是菱形，求BE的长．
一艘轮船以24海里∕小时的速度离开港口向东南方向航行，另一艘轮船同时以10海里∕小时的速度离开港口向西南方向航行，经过1小时，这两艘轮船相距多远？
如图，在边长为1的小正方形组成的网格中画出一个格点三角形（三角形的各顶点都在方格的顶点上），使这个三角形的三边分别为
13
，
5
，2
5
，并求出这个三角形的面积．
在数轴上作出-
10
的对应点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网