Question

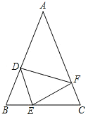
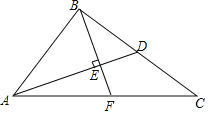
【题目】如图，在Rt△ACB中，∠ABC＝90°，D为BC边的中点，BE⊥AD于点E，交AC于F，若AB＝4，BC＝6，则线段EF的长为_____．

Answer 1

【答案】

【解析】

根据D为BC的中点和BC＝6，可以得到BD的长，然后根据∠ABC＝90°，AB＝4，利用勾股定理可以得到AD的长，再根据等积法可以求得BE的长，从而可以得到AE的长，根据DG∥BF，再利用三角形相似，即可求得EF的长．

解：过点D作DG∥BF交AC于点G，如图所示，

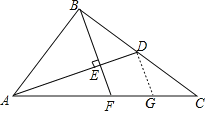
∵D为BC边的中点，BC＝6，

∴BD＝3，

在Rt△ACB中，∠ABC＝90°，AB＝4，

∴AD＝＝5，

∵BE⊥AD于点E，交AC于F，

∴BE＝，

∵AB＝4，BE＝，∠AEB＝90°，

∴AE＝，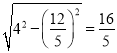

设DG＝x，则BF＝2x，EF＝2x﹣，

∵EF∥DG，

∴△AEF∽△ADG，

∴，即，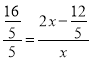

解得，x＝，

∴EF＝2x﹣＝2×﹣＝，

故答案为：．