题目内容
 如图,已知反比例函数
如图,已知反比例函数 在第一象限内的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.
在第一象限内的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.
(1)用含m的代数式表示四边形ODBE的面积;
(2)若y关于x的函数y=(2m-1)x2-2(m+1)x+m+3的图象与x轴只有一个交点,求四边形ODBE的面积.
解:(1)设点B(a,b),则点M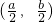 ,
,
∵反比例函数 在第一象限内的图象经过矩形OABC对角线的交点M,
在第一象限内的图象经过矩形OABC对角线的交点M,
∴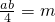 ,
,
∴ab=4m,
∴S四边形ODBE=S矩形OABC-S△OAD-S△OCE=4m- m-
m- m=3m;
m=3m;
(2)①当2m-1=0时,得m= ,
,
关于x的函数为一次函数:y=-3x+ ,
,
此时图象与x轴只有一个交点,且S四边形ODBE=3m= ;
;
②当2m-1≠0时,关于x的函数为二次函数,
∵y关于x的函数y=(2m-1)x2-2(m+1)x+m+3的图象与x轴只有一个交点,
∴△=[-2(m+1)]2-4(2m-1)(m+3)=-4m2-12m+16=0,
解得:m=1或m=-4,
∵m>0,
∴m=1,
∴此时S四边形ODBE=3m=3.
综上可得:四边形ODBE的面积为 或3.
或3.
分析:(1)首先设点B(a,b),可得点M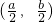 ,又由反比例函数
,又由反比例函数 在第一象限内的图象经过矩形OABC对角线的交点M,可得ab=4m,然后由S四边形ODBE=S矩形OABC-S△OAD-S△OCE,即可求得答案;
在第一象限内的图象经过矩形OABC对角线的交点M,可得ab=4m,然后由S四边形ODBE=S矩形OABC-S△OAD-S△OCE,即可求得答案;
(2)分别从2m-1=0与2m-1≠0去分析求解即可求得答案.
点评:此题考查了反比例函数的性质、一次函数的性质以及二次函数的性质.此题难度较大,注意掌握方程思想与数形结合思想的应用.
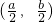 ,
,∵反比例函数
 在第一象限内的图象经过矩形OABC对角线的交点M,
在第一象限内的图象经过矩形OABC对角线的交点M,∴
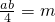 ,
,∴ab=4m,
∴S四边形ODBE=S矩形OABC-S△OAD-S△OCE=4m-
 m-
m- m=3m;
m=3m;(2)①当2m-1=0时,得m=
 ,
,关于x的函数为一次函数:y=-3x+
 ,
,此时图象与x轴只有一个交点,且S四边形ODBE=3m=
 ;
;②当2m-1≠0时,关于x的函数为二次函数,
∵y关于x的函数y=(2m-1)x2-2(m+1)x+m+3的图象与x轴只有一个交点,
∴△=[-2(m+1)]2-4(2m-1)(m+3)=-4m2-12m+16=0,
解得:m=1或m=-4,
∵m>0,
∴m=1,
∴此时S四边形ODBE=3m=3.
综上可得:四边形ODBE的面积为
 或3.
或3.分析:(1)首先设点B(a,b),可得点M
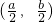 ,又由反比例函数
,又由反比例函数 在第一象限内的图象经过矩形OABC对角线的交点M,可得ab=4m,然后由S四边形ODBE=S矩形OABC-S△OAD-S△OCE,即可求得答案;
在第一象限内的图象经过矩形OABC对角线的交点M,可得ab=4m,然后由S四边形ODBE=S矩形OABC-S△OAD-S△OCE,即可求得答案;(2)分别从2m-1=0与2m-1≠0去分析求解即可求得答案.
点评:此题考查了反比例函数的性质、一次函数的性质以及二次函数的性质.此题难度较大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=