题目内容
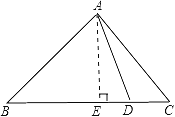
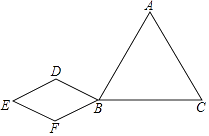
【题目】如图,B、D为线段AH上两点,△ABC、△BDE和△DGH都是等边三角形,连结CE并延长交AH的延长线于点F,点G恰好在CF上,△ABC的外接圆⊙O交CF于点M.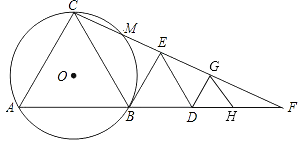
(1)求证:AC 2=CMCF;
(2)若CM= ![]() ,MF=
,MF= ![]() ,求圆O的半径长;
,求圆O的半径长;
(3)设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3 , 请直接写出S1、S2、S3之间的等量关系.
【答案】
(1)解:连结MB,则∠CMB=180°﹣∠A=120°,
∵∠CBF=60°+60°=120°,
∴∠CMB=∠CBF,
∵∠BCM=∠FCB,
∴△CMB∽△CBF,
∴ ![]() ,即CB2=CMCF,
,即CB2=CMCF,
∵AC=CB,
∴AC2=CMCF
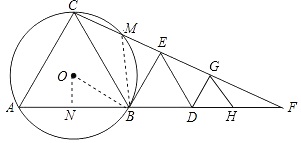
(2)解:过点O作ON⊥AB于点N,
则∠CMB=120°,
∵∠CBF=120°,
∴∠CMB=∠CBF,
∵∠BCF=∠BCM,
∴△CMB∽△CBF,
∴ ![]() =
= ![]() ,
,
即CB2=CMCF,
∵AC=CB=AB,CM= ![]() ,MF=
,MF= ![]() ,
,
∴CB2= ![]() ,
,
AB=AC=BC= ![]() ,
,
∵△ABC是等边三角形,
∴∠OBA=30°,
∴ON= ![]() BO,
BO,
∴cos30°= ![]() =
= ![]() =
= ![]() ,
,
解得:BO= ![]() ,
,
即⊙O的半径为: ![]() ;
;
(3)解:由题意可得:AC∥BE∥DG,BC∥DE∥HG,
∴ ![]() =
= ![]() =
= ![]()
∵ ![]() =(
=( ![]() )2
)2
![]() =(
=( ![]() )2
)2
∴ ![]() =
= ![]() 即S22=S1S3
即S22=S1S3
∴所求的数量关系是S22=S1S3.
【解析】1)连结MB易证∠CMB=∠CBF,则可以得到△CMB∽△CBF,根据相似三角形对应边的比相等即可证明;
(2)过点O作ON⊥AB于点N,易证∠CMB=∠CBF,则可以得到△CMB∽△CBF,根据相似三角形对应边的比相等即可得AB=AC=BC,从而得出△ABC是等边三角形,故∠OBA=30°,根据含30![]() 直角三角形的边之间的关系得出ON=
直角三角形的边之间的关系得出ON= ![]() BO,根据特殊锐角的三角函数值及锐角三角函数的定义列出方程求解即可;
BO,根据特殊锐角的三角函数值及锐角三角函数的定义列出方程求解即可;
(3)由题意可得:AC∥BE∥DG,BC∥DE∥HG,根据平行线分线段成比例定理及相似三角形的性质即可得出结论。
【考点精析】认真审题,首先需要了解平行线分线段成比例(三条平行线截两条直线,所得的对应线段成比例),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.

【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) |
|
|
|
汽车运费(元/辆) |
|
|
|
(1)若全部物资都用甲、乙两种车型来运送,需运费![]() 元,问分别需甲、乙两种车型各几辆?
元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知他们的总辆数为![]() 辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出哪种方案的运费最省?最省是多少元?