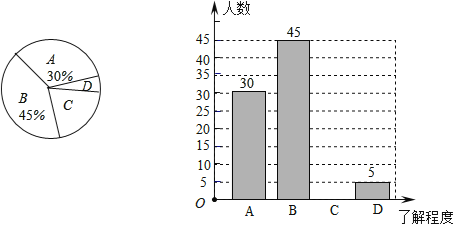
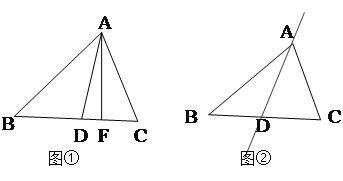题目内容
【题目】问题情境
(1)如图①,已知![]() ,试探究直线
,试探究直线![]() 与
与![]() 有怎样的位置关系?并说明理由.
有怎样的位置关系?并说明理由.
小明给出下面正确的解法:
直线![]() 与
与![]() 的位置关系是
的位置关系是![]() .
.
理由如下:
过点![]() 作
作![]() (如图②所示)
(如图②所示)
所以![]() (依据1)
(依据1)
因为![]() (已知)
(已知)
所以![]()
所以![]()
所以![]() (依据2)
(依据2)
因为![]()
所以![]() (依据3)
(依据3)
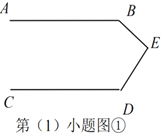
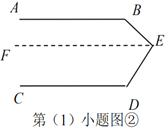
交流反思
上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?
“依据1”:________________________________;
“依据2”:________________________________;
“依据3”:________________________________.
类比探究
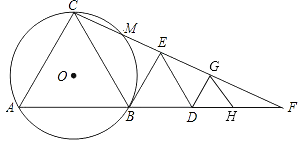
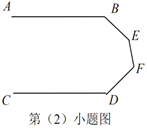
(2)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件________时,有
满足条件________时,有![]() .
.
拓展延伸
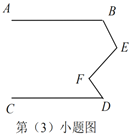
(3)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件_________时,有
满足条件_________时,有![]() .
.
【答案】(1)两直线平行,同旁内角互补;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;(2)∠B+∠E+∠F+∠D=540°;(3)∠B+∠E+∠D-∠F=180°.
【解析】
(1)根据平行线的性质和判定,平行公理的推论回答即可;
(2)过点E、F分别作GE∥HF∥CD,根据两直线平行,同旁内角互补及已知条件求得同旁内角∠ABE+∠BEG=180°,得到AB∥GE,再根据平行线的传递性来证得AB∥CD;
(3)过点E、F分别作ME∥FN∥CD,根据两直线平行,内错角相等及已知条件求得同旁内角∠B+∠BEM=180°,得到AB∥ME,再根据平行线的传递性来证得AB∥CD.
解:(1)由题意可知:“依据1”:两直线平行,同旁内角互补;
“依据2”: 同旁内角互补,两直线平行;
“依据3”: 如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD.
理由:如图,过点E、F分别作GE∥HF∥CD,
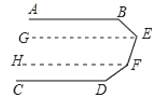
则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠BEF+∠EFD+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB∥GE,
∴AB∥CD;
(3)当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠D-∠F=180°时,有AB∥CD.
如图,过点E、F分别作ME∥FN∥CD,
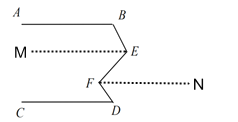
则∠MEF=EFN,∠D=∠DFN,
∵∠B+∠BEF+∠D-∠EFD=180°,
∴∠B+∠BEM+∠MEF+∠D-∠EFN-∠DFN=180°,
∴∠B+∠BEM=180°,
∴AB∥ME,
∴AB∥CD.

 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案