题目内容
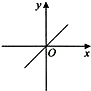
【题目】阅读下列内容,并答题:我们知道,计算n边形的对角线条数公式为: ![]() n(n﹣3).
n(n﹣3).
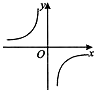
如果一个n边形共有20条对角线,那么可以得到方程 ![]() .
.
整理得n2﹣3n﹣40=0;解得n=8或n=﹣5
∵n为大于等于3的整数,∴n=﹣5不合题意,舍去.
∴n=8,即多边形是八边形.
根据以上内容,问:
(1)若一个多边形共有14条对角线,求这个多边形的边数;
(2)A同学说:“我求得一个多边形共有10条对角线”,你认为A同学说法正确吗?为什么?
【答案】
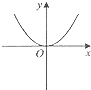
(1)解:根据题意得: ![]() n(n﹣3)=14,
n(n﹣3)=14,
整理得:n2﹣3n﹣28=0,
解得:n=7或n=﹣4.
∵n为大于等于3的整数,
∴n=﹣4不合题意,舍去.
∴n=7,即多边形是七边形.
(2)解:A同学说法是不正确的,理由如下:
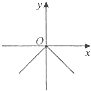
当 ![]() n(n﹣3)=10时,整理得:n2﹣3n﹣20=0,
n(n﹣3)=10时,整理得:n2﹣3n﹣20=0,
解得:n= ![]() ,
,
∴符合方程n2﹣3n﹣20=0的正整数n不存在,
∴多边形的对角线不可能有10条.
【解析】(1)利用“n边形的对角线条数公式”构建方程;(2)先假设再求根,不是整数,判断出不存在.

练习册系列答案
相关题目