Question

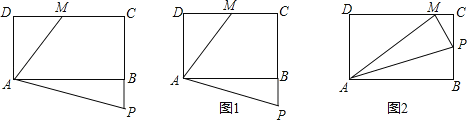
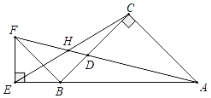
【题目】如图，点A、B、E在同一直线上，∠FEB＝∠ACB＝90°，AC＝BC，EB＝EF，连AF，CE交于点H，AF、CB交于点D，若tan∠CAD＝，则＝（　　）

A.B.C.D.

Answer 1

【答案】A

【解析】

如图，作CT⊥AB于T交AF于K．在Rt△ACD中，tan∠CAD＝，可以假设CD＝2a，AC＝3a，则BC＝AC＝3a．BD＝a，AB＝3a，BT＝AT＝a，想办法用a的代数式表示EF，FH即可解决问题．

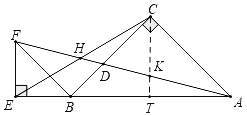
解：如图，作CT⊥AB于T交AF于K．

∵在Rt△ACD中，tan∠CAD＝，

∴可以假设CD＝2a，AC＝3a，

则BC＝AC＝3a．BD＝a，AB＝3a，BT＝AT＝a，

∵∠FEB＝∠ACB＝90°，AC＝BC，EB＝EF，

∴∠EBF＝∠CAB＝45°，

∴BF∥AC，

∴BF：AC＝BD：CD＝1：2，

∴BF＝a，

∴BE＝EF＝a，

∵TK∥EF，

∴TK：EF＝AT：AE，

∴TK：，

∴TK＝，

∴CK＝CT﹣TK＝，

由勾股定理可得AF＝，

AK＝，

∴FK＝AF﹣AK＝，

∵CK∥EF，

∴，

∴，

∴，

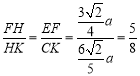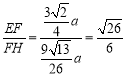故选：A．