题目内容
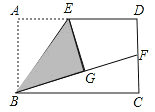
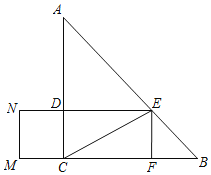
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC=3cm,点D为AC边上一点(不与点A、C重合),以CD为边,在三角形内作矩形CDEF,在三角形外作正方形CDMN,且顶点E、F分别在边AB、BC上,连接CE.设AD的长为xcm,矩形EFMN的面积为y1cm2,△ACE的面积为y2cm2
(1)填空:y1与x的函数关系式是 ,y2与x的函数关系式是 ,自变量x的取值范围是 ;
(2)在平面直角坐标系中,画出这两个函数的图象;
(3)结合画出的函数图象,解决问题:当矩形EFNM的面积小于△ACE的面积时,x的取值范围是 .
【答案】(1)y1=﹣3x+9,y2=![]() x,0<x<3;(2)见解析;(3)2<x<3
x,0<x<3;(2)见解析;(3)2<x<3
【解析】
(1)证出△ADE是等腰直角三角形,得出DE=AD=x,求出CD=AC﹣AD=3﹣x,由正方形的性质得出MN=DN=CD=3﹣x,EN=AC=3,由矩形和三角形面积公式即可得出y1=﹣3x+9,y2=![]() x;自变量x的取值范围是0<x<3;
x;自变量x的取值范围是0<x<3;
(2)由函数关系式和自变量的取值范围画出图象即可;
(3)求出两函数交点,结合图象即可得出答案.
解:(1)∵∠ACB=90°,AC=BC=3,
∴△ABC是等腰直角三角形,
∴∠A=45°,
∵四边形CDEF是矩形,
∴∠CDE=90°,
∴∠ADE=90°,
∴△ADE是等腰直角三角形,
∴DE=AD=x,
∴CD=AC﹣AD=3﹣x,
∵四边形CDMN是正方形,
∴MN=DN=CD=3﹣x,
∴EN=AC=3,
∴矩形EFMN的面积为y1=EN×MN=3(3﹣x)=﹣3x+9,即y1=﹣3x+9;
△ACE的面积为y2=![]() AC×DE=
AC×DE=![]() ×3x=
×3x=![]() x;即y2=
x;即y2=![]() x;
x;
自变量x的取值范围是0<x<3;
故答案为:y1=﹣3x+9,y2=![]() x,0<x<3;
x,0<x<3;
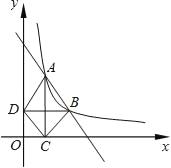
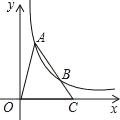
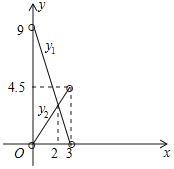
(2)两个函数的图象是不包括两个端点的线段,如图所示:
(3)令y1=y2,﹣3x+9=![]() x解得x=2
x解得x=2
由图象可知,当矩形EFNM的面积小于△ACE的面积时,x的取值范围是2<x<3;
故答案为:2<x<3.

【题目】某商场出售一批进价为2元的贺卡,在营运中发现此商品的日销价x(单位:元)与销售量y(单位:张)之间有如下关系:
x/元 | 3 | 4 | 5 | 6 |
y/张 | 20 | 15 | 12 | 10 |
(1)猜测并确定y与x的函数关系式.
(2)当日销售单价为10元时,贺卡的日销售量是多少张?
(3)设此卡的利润为W元,试求出W与x之间的函数关系式,若物价部门规定此卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大并求出最大的利润.