题目内容
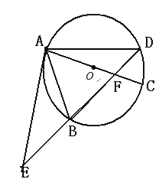
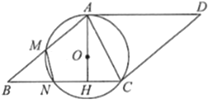
【题目】如图,点O是线段AH上一点,AH=3,以点O为圆心,OA的长为半径作⊙O,过点H作AH的垂线交⊙O于C,N两点,点B在线段CN的延长线上,连接AB交⊙O于点M,以AB,BC为边作ABCD.
(1)求证:AD是⊙O的切线;
(2)若OH![]() AH,求四边形AHCD与⊙O重叠部分的面积;
AH,求四边形AHCD与⊙O重叠部分的面积;
(3)若NH![]() AH,BN
AH,BN![]() ,连接MN,求OH和MN的长.
,连接MN,求OH和MN的长.
【答案】(1)证明见解析;(2)![]() ;(3)OH
;(3)OH![]() ,MN
,MN![]() .
.
【解析】
(1)根据平行四边形的性质可知AD∥BC,证明OA⊥AD,又因为OA为半径,即可证明结论;
(2)利用锐角三角函数先求出∠OCH=30°,再求出扇形OAC的面积,最后求出△OHC的面积,两部分面积相加即为重叠部分面积;
(3)设⊙O半径OA=r=OC,OH=3-r,在Rt△OHC中,利用勾股定理求出半径r=![]() ,推出OH=
,推出OH=![]() ,再在Rt△ABH和Rt△ACH中利用勾股定理分别求出AB,AC的长,最后证△BMN∽△BCA,利用相似三角形对应边的比相等即可求出MN的长.
,再在Rt△ABH和Rt△ACH中利用勾股定理分别求出AB,AC的长,最后证△BMN∽△BCA,利用相似三角形对应边的比相等即可求出MN的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠AHC=90°,
∴∠HAD=90°,即OA⊥AD,
又∵OA为半径,
∴AD是⊙O的切线;
(2)如图,连接OC,
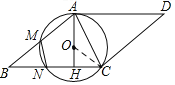
∵OH![]() OA,AH=3,
OA,AH=3,
∴OH=1,OA=2,
∵在Rt△OHC中,∠OHC=90°,OH![]() OC,
OC,
∴∠OCH=30°,
∴∠AOC=∠OHC+∠OCH=120°,
∴S扇形OAC![]() ,
,
∵CH![]() ,
,
∴S△OHC![]() 1
1![]() ,
,
∴四边形ABCD与⊙O重叠部分的面积=S扇形OAC+S△OHC![]() ;
;
(3)设⊙O半径OA=r=OC,OH=3﹣r,
在Rt△OHC中,OH2+HC2=OC2,
∴(3﹣r)2+12=r2,
∴r![]() ,则OH
,则OH![]() ,
,
在Rt△ABH中,AH=3,BH![]() 1
1![]() ,则AB
,则AB![]() ,
,
在Rt△ACH中,AH=3,CH=NH=1,得AC![]() ,
,
在△BMN和△BCA中,
∠B=∠B,∠BMN=∠BCA,
∴△BMN∽△BCA,
∴![]() 即
即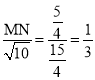 ,
,
∴MN![]() ,
,
∴OH![]() ,MN
,MN![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案