题目内容
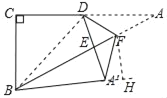
【题目】如图,在Rt△ABC中,∠C=90°,AC=4![]() ,BC=4,点D是AC的中点,点F是边AB上一动点,沿DF所在直线把△ADF翻折到△A′DF的位置,若线段A′D交AB于点E,且△BA′E为直角三角形,则BF的长为_____.
,BC=4,点D是AC的中点,点F是边AB上一动点,沿DF所在直线把△ADF翻折到△A′DF的位置,若线段A′D交AB于点E,且△BA′E为直角三角形,则BF的长为_____.

【答案】6或![]()
【解析】
由三角函数得出∠A=30°,由直角三角形的性质得出AB=2BC=8,由折叠的性质得出DA=DC=![]() ,FA′=FA,∠DA′F=∠A=30°,设BF=x,则AF=8﹣x,FA′=8﹣x,①当∠BEA′=90°时,由三角函数得出AE=3,得出EF=3﹣(8﹣x)=x﹣5,由直角三角形的性质得出方程,解方程即可;
,FA′=FA,∠DA′F=∠A=30°,设BF=x,则AF=8﹣x,FA′=8﹣x,①当∠BEA′=90°时,由三角函数得出AE=3,得出EF=3﹣(8﹣x)=x﹣5,由直角三角形的性质得出方程,解方程即可;
②当∠BA'E=90°时,作FH⊥BA',交BA'的延长线于H,连接BD,证明Rt△BDA'≌Rt△BDC,得出BA′=BC=4,求出∠FA'H=60°,在Rt△BFH中,由勾股定理得出方程,解方程即可.
解:∵∠C=90°,AC=![]() ,BC=4,
,BC=4,
∴tanA=![]() ,
,
∴∠A=30°,
∴AB=2BC=8,
∵点D是AC的中点,沿DF所在直线把△ADF翻折到△A′DF的位置,线段A′D交AB于点E,
∴DA=DC=![]() ,FA′=FA,∠DA′F=∠A=30°,
,FA′=FA,∠DA′F=∠A=30°,
设BF=x,则AF=8﹣x,FA′=8﹣x,
①当∠BEA′=90°时,在Rt△ADE中,cosA=![]() ,
,
∴AE=![]() ×cos30°=3,
×cos30°=3,
∴EF=3﹣(8﹣x)=x﹣5,
在Rt△A'FE中,∵∠FA'E=30°,
∴FA'=2FE,即8﹣x=2(x﹣5),
解得x=6,即BF=6;
②当∠BA'E=90°时,作FH⊥BA',交BA'的延长线于H,连接BD,如图所示:
在Rt△BDA'和△BDC中,![]() ,
,
∴Rt△BDA'≌Rt△BDC(HL),
∴BA′=BC=4,
∵∠BA'F=∠BA'E+∠FA'E=90°+30°=120°,
∴∠FA'H=60°,
在Rt△FHA'中,A′H=![]() A′F=
A′F=![]() (8﹣x),FH=
(8﹣x),FH=![]() A′H=
A′H=![]() (8﹣x),
(8﹣x),
在Rt△BFH中,∵FH2+BH2=BF2,
∴![]() (8﹣x)2+[
(8﹣x)2+[![]() (8﹣x)+4]2=x2,
(8﹣x)+4]2=x2,
解得:x=![]() ,即BF=
,即BF=![]() .
.
综上所述,BF的长为6或![]() .
.
故答案为:6或![]() .
.