��Ŀ����
����Ŀ������֪�������һ�����εĿ��볤֮��Ϊ![]() ����ô������ξͳ�Ϊ�ƽ���Σ���ͼ����֪A��B���㶼�ڷ���������y��
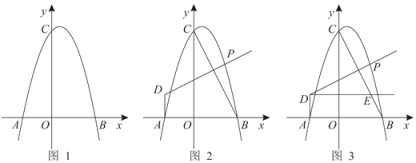
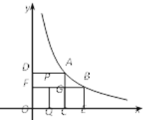
����ô������ξͳ�Ϊ�ƽ���Σ���ͼ����֪A��B���㶼�ڷ���������y��![]() ��k��0��λ�ڵ�һ�����ڵ�ͼ���ϣ���A��B����ֱ���������Ĵ��ߣ�����ֱ�ΪC��D��E��F����AC��BF���ڵ�G����֪�ı���OCAD��CEBG��������������FG��OC���е�ֱ�ΪP��Q������PQ���������½��ۣ����ı���ADFGΪ�ƽ���Σ����ı���OCGFΪ�ƽ���Σ����ı���OQPFΪ�ƽ���Σ����Ͻ����У���ȷ���ǣ� ��
��k��0��λ�ڵ�һ�����ڵ�ͼ���ϣ���A��B����ֱ���������Ĵ��ߣ�����ֱ�ΪC��D��E��F����AC��BF���ڵ�G����֪�ı���OCAD��CEBG��������������FG��OC���е�ֱ�ΪP��Q������PQ���������½��ۣ����ı���ADFGΪ�ƽ���Σ����ı���OCGFΪ�ƽ���Σ����ı���OQPFΪ�ƽ���Σ����Ͻ����У���ȷ���ǣ� ��
A. ��B. ��C. �ڢ�D. �٢ڢ�
���𰸡�B
��������
��A(![]() ),B(
),B(![]() ),
),![]() ,�ٸ��ݻƽ���εĶ�����.
,�ٸ��ݻƽ���εĶ�����.
��A(![]() ),B(
),B(![]() ),
),![]() ,���ı���OCADΪ�����Σ���
,���ı���OCADΪ�����Σ���![]() =
=![]() ����
����![]() ��
��![]() =
=![]() =
=![]() ����A(
����A(![]() ��
��![]() )����CEBG��������
)����CEBG��������![]() ����
����![]() -
-![]() =
=![]() ������
������![]() ��
��![]() ��
��![]() ����B(
����B(![]() ,
,![]() ),G������(
),G������(![]() ,
,![]() ), Q�������(
), Q�������(![]() ,0),ƽ���ı���/span>ADFG�У�
,0),ƽ���ı���/span>ADFG�У�![]() �����ı���OCGF�У�
�����ı���OCGF�У�![]() ���ı���OQPF�У�
���ı���OQPF�У�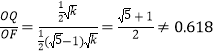 ����ѡB.
����ѡB.

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ