题目内容
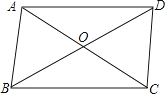
【题目】如图,△ABC与△ABD中,AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
你添加的条件是?并证明。
【答案】解:添加条件例举:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等.
证明:①如果添加条件是AD=BC时,
∵BC=AD,∠2=∠1,AB=BA,
在△ABC与△BAD中, ,
,
∴△ABC≌△BAD,
∴AC=BD;
②如果添加条件是OC=OD时,
∵∠1=∠2
∴OA=OB
∴OA+OD=OB+OD
∴BC=AD
又∵∠2=∠1,AB=BA
在△ABC与△BAD中,  ,
,
∴△ABC≌△BAD,
∴AC=BD;
③如果添加条件是∠C=∠D时,
∵∠2=∠1,AB=BA,
在△ABC与△BAD中, ,
,
∴△ABC≌△BAD,
∴AC=BD;
④如果添加条件是∠CAO=∠DBC时,
∵∠1=∠2,
∴∠CAO+∠1=∠DBC+∠2,
∴∠CAB=∠DBA,
又∵AB=BA,∠2=∠1,
在△ABC与△BAD中,  ,
,
∴△ABC≌△BAD,
∴AC=BD.
故答案为:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC.
【解析】要使AC=BD,可以证明△ACB≌△BDA或者△ACO≌△BDO从而得到结论.

练习册系列答案
相关题目