题目内容
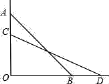
【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
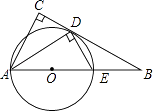
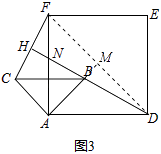
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3 ![]() 时,求线段DH的长.
时,求线段DH的长.
【答案】
(1)
解:BD=CF.
理由如下:由题意得,∠CAF=∠BAD=θ,
在△CAF和△BAD中,
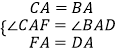 ,
,
∴△CAF≌△BAD,
∴BD=CF;
(2)
解:①由(1)得△CAF≌△BAD,
∴∠CFA=∠BDA,
∵∠FNH=∠DNA,∠DNA+∠NAD=90°,
∴∠CFA+∠FNH=90°,
∴∠FHN=90°,即BD⊥CF;
②连接DF,延长AB交DF于M,
∵四边形ADEF是正方形,AD=3 ![]() ,AB=2,
,AB=2,
∴AM=DM=3,BM=AM﹣AB=1,
DB= ![]() =
= ![]() ,
,
∵∠MAD=∠MDA=45°,
∴∠AMD=90°,又∠DHF=90°,∠MDB=∠HDF,
∴△DMB∽△DHF,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,DH= ![]() .
.
【解析】本题考查的是正方形的性质、等腰直角三角形的性质、旋转变换的性质以及相似三角形的判定和性质,掌握旋转角的定义和旋转变换的性质、正确作出辅助性是解题的关键.(1)根据旋转变换的性质和全等三角形的判定定理证明△CAF≌△BAD,证明结论;(2)①根据全等三角形的性质、垂直的定义证明即可;②连接DF,延长AB交DF于M,根据题意和等腰直角三角形的性质求出DM、BM的长,根据勾股定理求出BD的长,根据相似三角形的性质列出比例式,计算即可得到答案.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目