题目内容
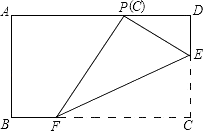
【题目】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为( )
A.5
B.7
C.8
D.![]()
【答案】B
【解析】解:作CH⊥AB于H,如图,
∵菱形ABCD的边AB=8,∠B=60°,
∴△ABC为等边三角形,
∴CH= ![]() AB=4
AB=4 ![]() ,AH=BH=4,
,AH=BH=4,
∵PB=3,
∴HP=1,
在Rt△CHP中,CP= ![]() =7,
=7,
∵梯形APQD沿直线PQ折叠,A的对应点A′,
∴点A′在以P点为圆心,PA为半径的弧上,
∴当点A′在PC上时,CA′的值最小,
∴∠APQ=∠CPQ,
而CD∥AB,
∴∠APQ=∠CQP,
∴∠CQP=∠CPQ,
∴CQ=CP=7.
故选B.
本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了折叠的性质.解决本题的关键是确定A′在PC上时CA′的长度最小.作CH⊥AB于H,如图,根据菱形的性质可判断△ABC为等边三角形,则CH= ![]() AB=4
AB=4 ![]() ,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可.
,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可.

【题目】东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p=  且其日销售量y(kg)与时间t(天)的关系如表:
且其日销售量y(kg)与时间t(天)的关系如表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.