Question

【题目】如图，在ABCD中，对角线AC、BD相交成的锐角为60°，若AC=6，BD=8，求ABCD的面积．（ ，结果精确到0.1）

Answer 1

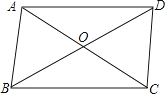
【答案】解：过A点作AE⊥BD于E点，如图所示：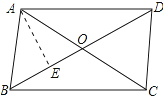

∵四边形ABCD是平行四边形
∴OA= AC=3，
在Rt△AEO中，∠AOE=60°，
∴AE=OAsin60°=3× = ，
∴S□ABCD=2S△ABD=2× BDAE=2× ×8× = ≈20.8．
【解析】作AE⊥BD于E，如图，根据平行四边形的性质得OA=OC= AC=3，△ABD≌△CDB，在Rt△AEO中，由三角函数求出AE，然后利用平行四边形ABCD的面积=2S△ABD进行计算即可．
【考点精析】本题主要考查了平行四边形的性质和解直角三角形的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能正确解答此题．