题目内容
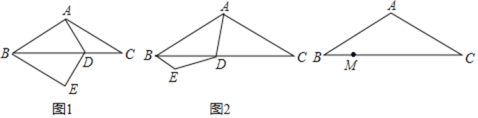
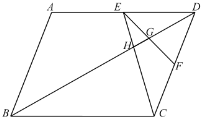
【题目】如图，
中，点
、
分别是边
、
的中点，
、
分别交对角线
于点
、
，则
______.
【答案】
【解析】
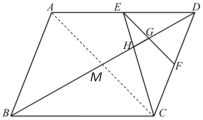
由四边形ABCD是平行四边形可得AD∥BC，AD=BC，△DEH∽△BCH，进而得
，连接AC，交BD于点M，如图，根据三角形的中位线定理可得EF∥AC，可推得
，△EGH∽△CMH，于是得DG=MG，
，设HG=a，依次用a的代数式表示出MH、DG、BH，进而可得答案.
解：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，
∴△DEH∽△BCH，∵E是AD中点，AD=BC，∴，
连接AC，交BD于点M，如图，∵点
、
分别是边
、
的中点，∴EF∥AC，
∴，△EGH∽△CMH，∴DG=MG，，
设HG=a，则MH=2a，MG=3a，∴DG=3a，∴DM=6a，
∵四边形ABCD是平行四边形，∴BM=DM=6a，BH=8a，
∴
.
故答案为：.
练习册系列答案
相关题目
