题目内容
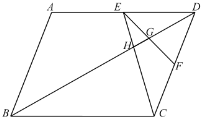
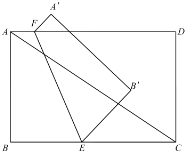
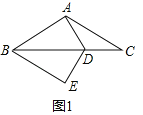
【题目】如图，△ABC中，AB＝AC＝2
，∠BAC＝120°，D为BC边上的点，将DA绕D点逆时针旋转120°得到DE．
（1）如图1，若AD＝DC，则BE的长为 ，BE2+CD2与AD2的数量关系为 ；
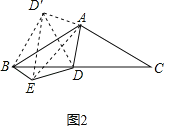
（2）如图2，点D为BC边山任意一点，线段BE、CD、AD是否依然满足（1）中的关系，试证明；
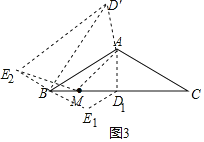
（3）M为线段BC上的点，BM＝1，经过B、E、D三点的圆最小时，记D点为D1，当D点从D1处运动到M处时，E点经过的路径长为 ．
【答案】（1）2
；BE2+CD2＝4AD2；（2）能满足（1）中的结论，见解析；（3）2
【解析】
（1）依据旋转性质可得：DE＝DA＝CD，∠BDE＝∠ADB＝60°，再证明：△BDE≌△BDA，利用勾股定理可得结论；
（2）将△ACD绕点A顺时针旋转120°得到△ABD′，再证明：∠D′BE＝∠D′AE＝90°，利用勾股定理即可证明结论仍然成立；
（3）从（2）中发现：∠CBE＝30°，即：点D运动路径是线段；分别求出点D位于D1时和点D运动到M时，对应的BE长度即可得到结论．
解：（1）如图1，∵AB＝AC，∠BAC＝120°，
∴∠ABC＝∠ACB＝30°，
∵AD＝DC
∴∠CAD＝∠ACB＝30°，∠ADB＝∠CAD+∠ACB＝60°，
∴∠BAD＝90°，
由旋转得：DE＝DA＝CD，∠BDE＝∠ADB＝60°
∴△BDE≌△BDA（SAS）
∴∠BED＝∠BAD＝90°，BE＝AB＝
∴BE2+CD2＝BE2+DE2＝BD2
∵
＝cos∠ADB＝cos60°＝
∴BD＝2AD
∴BE2+CD2＝4AD2；
故答案为：；BE2+CD2＝4AD2；
（2）能满足（1）中的结论．如图2，将△ACD绕点A顺时针旋转120°得到△ABD′，使AC与AB重合，
∵∠DAD′＝120°，∠BAD′＝∠CAD，∠ABD′＝∠ACB＝30°，AD′＝AD＝DE，∠DAE＝∠AED＝30°，BD′＝CD，∠AD′B＝∠ADC
∴∠D′AE＝90°
∵∠ADB+∠ADC＝180°
∴∠ADB+∠AD′B＝180°
∴A、D、B、D′四点共圆，
同理可证：A、B、E、D四点共圆，A、E、B、D′四点共圆；
∴∠D′BE＝90°
∴BE2+BD′2＝D′E2
∵在△AD′E中，∠AED′＝30°，∠EAD′＝90°
∴D′E＝2AD′＝2AD
∴BE2+BD′2＝（2AD）2＝4AD2
∴BE2+CD2＝4AD2．
（3）由（2）知：经过B、E、D三点的圆必定经过D′、A，且该圆以D′E为直径，
该圆最小即D′E最小，∵D′E＝2AD
∴当AD最小时，经过B、E、D三点的圆最小，此时，AD⊥BC
如图3，过A作AD1⊥BC于D1，∵∠ABC＝30°
∴BD1＝ABcos∠ABC＝cos30°＝3，AD1＝
∴D1M＝BD1﹣BM＝3﹣1＝2
由（2）知：在D运动过程中，∠CBE＝30°，∴点D运动路径是线段；
当点D位于D1时，由（2）中结论得：
，∴BE1＝
当点D运动到M时，易求得：BE2＝
∴E点经过的路径长＝BE1+BE2＝2
故答案为：2．
