Question

【题目】图1所示的是某超市入口的双翼闸门，如图2，当它的双翼展开时，双翼边缘的端点A与B 之间的距离为10cm，双翼的边缘AC=BD=54cm，且与闸机侧立面夹角∠PCA=∠BDQ=30°，求当双翼收起时，可以通过闸机的物体的最大宽度。

Answer 1

【答案】64cm.

【解析】

根据题意过点A作AE⊥CP于点E，过点B作BF⊥DQ于点F，然后在直角三角形中利用三角函数求出AE和BF，从而可求出通过闸机的物体的最大宽度.

解：如图所示：

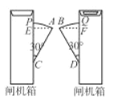
过点A作AE⊥CP于点E，过点B作BF⊥DQ于点F，

在RT△ACE中，AE=sin30°×AC=×54=27cm，

同理可得BF=27cm,

又∵点A与B之间的距离为10cm,

∴通过闸机的物体的最大宽度为：27+10+27=64cm,

答：通过闸机的物体的最大宽度为：64cm.