题目内容
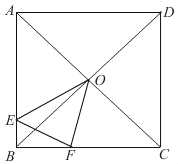
【题目】如图,O为正方形ABCD对角线的交点,E为AB边上一点,F为BC边上一点,△EBF的周长等于BC的长.
(1)若AB=12,BE=3,求EF的长;
(2)求∠EOF的度数;
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.
【答案】(1)EF =5;(2)∠EOF=45°;(3)![]() .
.
【解析】
(1)设BF=x,则FC=BC﹣BF=12﹣x,根据BE=3,且BE+BF+EF=BC,表示出
EF,在Rt△BEF中,根据勾股定理即可求出![]() ,即可求出EF的长;
,即可求出EF的长;
(2)如图,在FC上截取FM=FE,连接OM,分别证明△OBE≌△OCM,△OFE≌△OFM,根据全等三角形的性质即可求出∠EOF的度数;
(3)证明△AOE∽△CFO.根据相似三角形的性质得到![]()
![]() 即可求出
即可求出![]() 的值.
的值.
(1)设BF=x,则FC=BC﹣BF=12﹣x,
∵BE=3,且BE+BF+EF=BC,
∴EF=9﹣x,
在Rt△BEF中,由BE2+BF2=EF2可得32+x2=(9﹣x)2,
解得:x=4,
则EF=9﹣x=5;
(2)如图,在FC上截取FM=FE,连接OM,

∵C△EBF的周长=BE+EF+BF=BC,则BE+EF+BF=BF+FM+MC,
∴BE=MC,
∵O为正方形中心,
∴OB=OC,∠OBE=∠OCM=45°,
在△OBE和△OCM中,
∵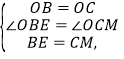
∴△OBE≌△OCM,
∴∠EOB=∠MOC,OE=OM,
∴∠EOB+∠BOM=∠MOC+∠BOM,即∠EOM=∠BOC=90°,
在△OFE与△OFM中,
∵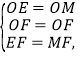
∴△OFE≌△OFM(SSS),
∴![]()
(3)证明:由(2)可知:∠EOF=45°,
∴∠AOE+∠FOC=135°,
∵∠EAO=45°,
∴∠AOE+∠AEO=135°,
∴∠FOC=∠AEO,
∵∠EAO=∠OCF=45°,
∴△AOE∽△CFO.
∴![]()
∴![]()
∵AO=CO,
∴![]()
∴![]()








