��Ŀ����
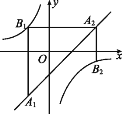
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y��ax2��![]() x+c��ֱ��y��
x+c��ֱ��y��![]() x+
x+![]() ����A��B���㣬��֪��B�ĺ�������4��ֱ��y��
����A��B���㣬��֪��B�ĺ�������4��ֱ��y��![]() x+
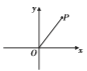
x+![]() ��x��y��Ľ���ֱ�ΪA��C����P����������һ���㣮
��x��y��Ľ���ֱ�ΪA��C����P����������һ���㣮
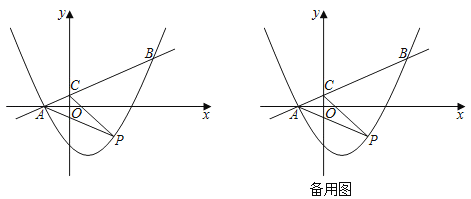
��1���������ߵĽ���ʽ��
��2������P��ֱ��y��![]() x+
x+![]() �·������PAC����������
�·������PAC����������
��3����M�������߶Գ����ϵ�һ�㣬�Ե�A��B��P��MΪ������ı����ܷ��Ϊƽ���ı��Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��y��![]() x2��
x2��![]() x��
x��![]() ����2��
����2��![]() ����3����P����������6��
����3����P����������6��![]() ����4��
����4��![]() ����2����
����2����![]() ����
����
��������
��1����ֱ��y��![]() x+
x+![]() ��x��y��Ľ���ֱ�ΪA��C���ó���A�����꣬��x=4����ֱ��y��
��x��y��Ľ���ֱ�ΪA��C���ó���A�����꣬��x=4����ֱ��y��![]() x+
x+![]() �����yֵ�����ɵó���B���꣬�ɵ�A��B������������ô���ϵ����������������ߵĽ���ʽ��
�����yֵ�����ɵó���B���꣬�ɵ�A��B������������ô���ϵ����������������ߵĽ���ʽ��
��2������P��y���ƽ���߽�AB�ڵ�H�����P�����꣬��ʾ��H�����꣬���÷ָ�ͼ�η�������ҳ�S��PAC����x�Ķ��κ�����ϵʽ�����ݶ��κ��������ʼ��ɽ����ֵ���⣻
��3�������ܣ����߶�ABΪ�Խ��ߺͱ�������������ǣ�����ƽ�Ƶ����ʺ��е㹫ʽ���P��ĺ����꣬������������߽���ʽ�м��ɵó���P�����꣮
�⣺��1��y��![]() x+
x+![]() ����y��0����x����1���ʵ�A����1��0����
����y��0����x����1���ʵ�A����1��0����
��B�������4�����B��4��2����
����A��B��������������߱���ʽ�ã�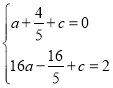 ����ã�
����ã�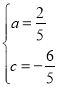 ��
��
�������ߵı���ʽΪ��y��![]() x2��
x2��![]() x��
x��![]() ��
��
��2������P��y���ƽ���߽�AB�ڵ�H��
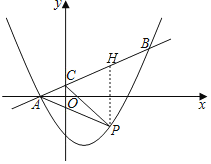
���P��x��![]() x2��
x2��![]() x��
x��![]() �������H��x��
�������H��x��![]() x+
x+![]() ��
��
���PAC���S��S��PHA��S��PHC��![]() PH��xC��xA��
PH��xC��xA��
��![]() ����
����![]() x+
x+![]() ��
��![]() x2+
x2+![]() x+
x+![]() ��
��
����![]() x2+
x2+![]() x+
x+![]() ��
��
��![]() ��0����S�����ֵ��
��0����S�����ֵ��
��x��![]() ʱ��S�����ֵΪ��
ʱ��S�����ֵΪ��![]() ��
��
��3���ܣ����ɣ�
���P������Ϊ����m��n������M��1��s��������A��B������ֱ�Ϊ������1��0������4��2����
�ٵ�AB�DZ�ʱ��
��A����ƽ��5����λ������ƽ��2����λ�õ�B��
ͬ������P��M������ƽ��5����λ������ƽ��2����λ�õ�M��P����
��1+5��m��1��5��m��
��ã�m��6��4����n��![]() ��
��
�ʵ�P��6��![]() ����4��
����4��![]() ����
����
�ڵ�AB�ǶԽ���ʱ��
���е㹫ʽ�ã�m+1��4��1��
��ã�m��2���ʵ�P��2����![]() ����
����
���ϣ���P������Ϊ����6��![]() ����4��
����4��![]() ����2����
����2����![]() ����
����

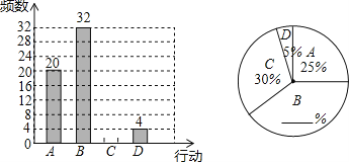
 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�����Ŀ���Ķ��������ݣ�����Ҫ�������⣺
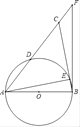
���⣺����ƽ���ڣ���֪�ֱ���2���㣬3���㣬4���㣬5���㣬����![]() ���㣬�������������㶼����ͬһ��ֱ���Ͼ���ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ���
���㣬�������������㶼����ͬһ��ֱ���Ͼ���ÿ���㻭һ��ֱ�ߣ����ǿ��Էֱ�����ֱ�ߣ���
̽����Ϊ�˽��������⣬ϣ��С���ͬѧ�ǣ���������±������̽������Ϊ�˷����о����⣬ͼ��ÿ���߶α�ʾ���߶����˵��һ��ֱ�ߣ�
���� | 2 | 3 | 4 | 5 | �� |
|
ʾ��ͼ |
|
|
|
| �� |
|
ֱ������ | 1 |
|
|
| �� |
�����������⣺
��1�������ϣ��С����ɣ���ֱ��д�����ۣ���ƽ������![]() ����ʱ��ֱ������Ϊ______��
����ʱ��ֱ������Ϊ______��
��2����ijͬѧ���ձ����еķ�����������28��ֱ�ߣ����ƽ�����ж��ٸ���֪�㣿