题目内容
【题目】如图，在平面直角坐标系中，将点
绕原点
按逆时针方向旋转
得到点
，则点的坐标为（ ）
A.
B.
C.
D.
【答案】C
【解析】
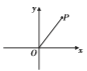
过点P作PA⊥x轴于点A，作P'B⊥x轴于点B，根据点P的坐标求出PA、OA的长度，根据旋转的性质得出P'O=OP，证明△P'OB≌△OPA，即可得解．
如图，过点P作PA⊥x轴于点A，作P'B⊥x轴于点B．
∵点P（3，4），∴PA=4，OA=3．
∵点P（3，4）绕坐标原点逆时针旋转90°得到点P'，
∴P'O=PO，P'O⊥PO，
∴∠P'OP=90°，
∴∠P'OB+∠POA=90°．
∵∠POA+∠OPA=90°，
∴∠P'OB=∠OPA．
∵∠P'OB=∠OPA，∠P'BO=∠OAP=90°，P'O=OP，
∴△P'OB≌△OPA，∴OB=PA=4，P'B=OA=3，
∴点P'的坐标是（﹣4，3）．
故选C．
练习册系列答案
相关题目
【题目】为了解某区八年级学生的睡眠情况，随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人，利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表（单位：小时）
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
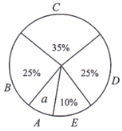
根据图表提供的信息，回答下列问题：
（1）试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数；
（2）如果睡眠时间x（时）满足：
，称睡眠时间合格.已知该区八年级学生有3250人，试估计该区八年级学生睡眠时间合格的共有多少人？
（3）如果将各组别学生睡眠情况分组的最小值（如C组别中，取
），B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
