题目内容
【题目】如图,反比例函数y= ![]() (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )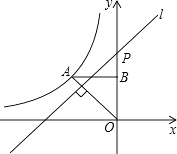
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:如图, 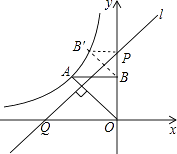
∵点A坐标为(﹣1,1),
∴k=﹣1×1=﹣1,
∴反比例函数解析式为y=﹣ ![]() ,
,
∵OB=AB=1,
∴△OAB为等腰直角三角形,
∴∠AOB=45°,
∵PQ⊥OA,
∴∠OPQ=45°,
∵点B和点B′关于直线l对称,
∴PB=PB′,BB′⊥PQ,
∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,
∴B′P⊥y轴,
∴点B′的坐标为(﹣ ![]() ,t),
,t),
∵PB=PB′,
∴t﹣1=|﹣ ![]() |=
|= ![]() ,
,
整理得t2﹣t﹣1=0,解得t1= ![]() ,t2=
,t2= ![]() (不符合题意,舍去),
(不符合题意,舍去),
∴t的值为 ![]() .
.
所以答案是:A.
【考点精析】解答此题的关键在于理解公式法的相关知识,掌握要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之,以及对坐标与图形变化-对称的理解,了解关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y).

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目