题目内容
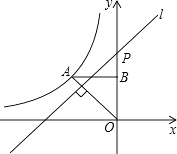
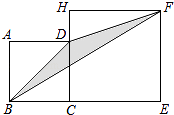
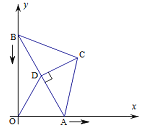
【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒4个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动.当△ABC的边与坐标轴平行时,t=_____________.
【答案】![]()
【解析】分析:分两种情况:①当CA⊥x轴时,根据两角对应相等的两三角形相似证明△CAD∽△ABO,得出![]() ,求出AO的值;②CB⊥y轴时,同理,可求出AO的值.
,求出AO的值;②CB⊥y轴时,同理,可求出AO的值.
详解:∵BC=AC,CD⊥AB,
∴D为AB的中点,
∴AD=![]() AB=4.
AB=4.
在Rt△CAD中,CD=![]() =3,
=3,
分两种情况:
①设AO=4t1时,CA⊥x轴时,A垂足,如图.
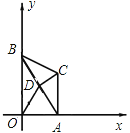
∴CA⊥OA,
∴CA∥y轴,
∴∠CAD=∠ABO.
又∵∠CDA=∠AOB=90°,
∴Rt△CAD∽Rt△ABO,
∴![]() ,即
,即![]() ,
,
解得t1=![]() ;
;
②设AO=4t2时,CB⊥y轴,B为切点,如图.
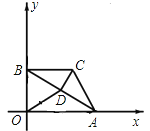
同理可得,t2=![]() .
.
综上可知,当以点C为圆心,CA为半径的圆与坐标轴相切时,t的值为![]() 或
或![]() .
.

练习册系列答案
相关题目