Question

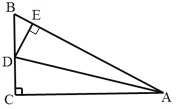
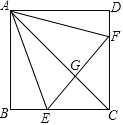
【题目】已知将一块直角三角板DEF放置在△ABC上，使得该三角板的两条直角边DE，DF恰好分别经过点B、C．

（1）∠DBC＋∠DCB＝ 度；

（2）过点A作直线直线MN∥DE，若∠ACD＝20°，试求∠CAM的大小．

Answer 1

【答案】（1）90；(2) 110°．

【解析】试题分析：（1）在中，根据三角形内角和定理得然后把代入计算即可；

结合上问易知，又MN∥DE，两直线平行，内错角相等可得∠ABD＝∠BAN．而，两式相减，即可求得.

试题解析：

（1）(1)在△DBC中,∵

而，

故答案为：90；

（2）由于三角形内角和为180°，

结合上问易知，

又MN∥DE，

∴∠ABD＝∠BAN．

而，

两式相减，得： ．而∠ACD＝20°，故∠CAM＝110°．