题目内容
【题目】矩形中![]() ,点
,点![]() 分别在边
分别在边![]() 上,点
上,点![]() 分别在边
分别在边![]() 上,
上,![]() 与
与![]() 交于点
交于点![]() ,记
,记![]() .
.
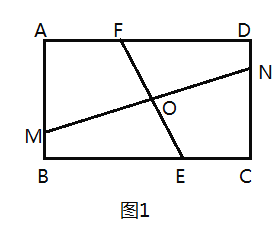
(1)如图1,当![]() 时,若
时,若![]() ,求
,求![]() 的值;
的值;
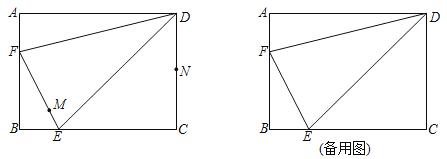
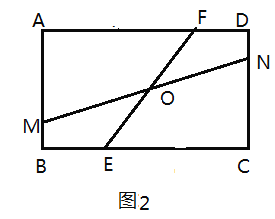
(2)如图2,当![]() 时,求
时,求![]() 的最大值和最小值;
的最大值和最小值;
(3)若![]() 的值为3,当
的值为3,当![]() 与
与![]() 重合且
重合且![]() 为直角三角形时,直接写出
为直角三角形时,直接写出![]() 的值.
的值.
【答案】(1)2;(2)当![]() 的长取最大时,
的长取最大时,![]() 取最短,此时
取最短,此时![]() 最大,最大值为
最大,最大值为![]() ;当
;当![]() 的最短时,
的最短时,![]() 的值取最大,此时
的值取最大,此时![]() 的值最小,最小值为
的值最小,最小值为![]() ;(3)
;(3)![]() 为
为![]() 或
或![]()
【解析】
(1)作![]() 于
于![]() 于
于![]() ,设
,设![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,易证
,易证![]() ,得
,得![]() ,进而即可求解;
,进而即可求解;
(2)设![]() ,则
,则![]() ,可得MN最短为
,可得MN最短为![]() ,最长为
,最长为![]() ,EF最短为
,EF最短为![]() ,最长为
,最长为![]() ,进而即可得到结论;
,进而即可得到结论;
(3)当![]() 与
与![]() 重合且
重合且![]() 为直角三角形时,分两种情况:①∠DFO=90°时,②当∠DOF=90°时,分别求解,即可.
为直角三角形时,分两种情况:①∠DFO=90°时,②当∠DOF=90°时,分别求解,即可.
(1)作![]() 于
于![]() 于
于![]() ,设
,设![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ;
;
(2)![]() ,
,
∴设![]() ,则
,则![]() ,
,
![]() 时,MN最短为
时,MN最短为![]() 与对角线重合时,MN最长为
与对角线重合时,MN最长为![]() ,
,
![]() 时,EF最短为
时,EF最短为![]() 与对角线重合时,EF最长为
与对角线重合时,EF最长为![]() ,
,
![]() ,
,
![]() 当
当![]() 的长取最大时,
的长取最大时,![]() 取最短,此时
取最短,此时![]() 最大,最大值为
最大,最大值为![]() ,
,
当![]() 的最短时,
的最短时,![]() 的值取最大,此时
的值取最大,此时![]() 的值最小,最小值为
的值最小,最小值为![]()
即![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ;
;
(3)∵![]() =3,
=3,
∴设EF=a,则MN=3a,
当![]() 与
与![]() 重合且
重合且![]() 为直角三角形时,分两种情况:
为直角三角形时,分两种情况:
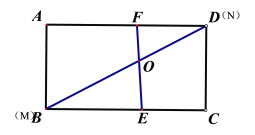
①∠DFO=90°时,AB=CD=EF=a,BD=MN=3a,
∴BC=![]() ,
,
∴![]() =a:
=a:![]() =
=![]() ;
;
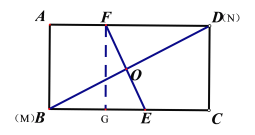
②当∠DOF=90°时,过点F作FG⊥BC于点G,
∴∠EFG+∠FEG=∠DBC+∠FEG,
∴∠EFG=∠DBC,
∵∠FGE=∠BCD=90°,
∴FGE~BCD,
∴![]() ,
,
∵FG=AB,
∴![]() =
=![]() ,
,
综上所述:![]() 为
为![]() 或
或![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目