题目内容
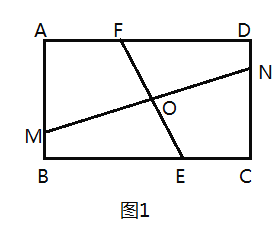
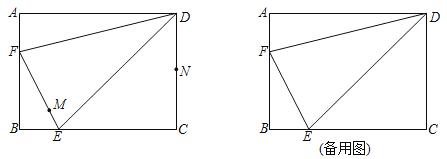
【题目】如图，在矩形ABCD中，AB＝6，BC＝8，点E，F分别在边BC，AB上，AF＝BE＝2，连结DE，DF．动点M在EF上从点E向终点F匀速运动，同时，动点N在射线CD上从点C沿CD方向匀速运动，当点M运动到EF的中点时，点N恰好与点D重合，点M到达终点时，M，N同时停止运动．
（1）求EF的长．
（2）设CN＝x，EM＝y，求y关于x的函数表达式，并写出自变量x的取值范围．
（3）连结MN，当MN与△DEF的一边平行时，求CN的长．
【答案】（1）EF=2
；（2）y＝
x（0≤x≤2）；（3）满足条件的CN的值为
或12．
【解析】
（1）在Rt△BEF中，利用勾股定理即可解决问题．
（2）根据速度比相等构建关系式解决问题即可．
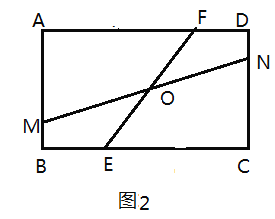
（3）分两种情形如图3﹣1中，当MN∥DF，延长FE交DC的延长线于H．如图3﹣2中，当MN∥DE，分别利用平行线分线段成比例定理构建方程解决问题即可．
解：（1）∵四边形ABCD是矩形，
∴∠B＝90°，AB＝CD＝6，AD＝BC＝8，
∵AF＝BE＝2，
∴BF＝6﹣2＝4，
∴EF＝
＝
＝2．
（2）由题意：
＝
，
∴＝
，
∴y＝x（0≤x≤2）．
（3）如图3﹣1中，延长FE交DC的延长线于H．
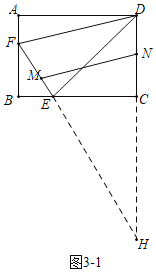
∵△EFB∽△EHC，
∴
＝
＝
，
∴
＝
＝
，
∴EH＝6，CH＝12，
当MN∥DF时，
＝
，
∴
＝
，
∵y＝x，
解得x＝，这种情形不存在．
如图3﹣2中，当MN∥DE时，
＝
，
∴
＝ 
，
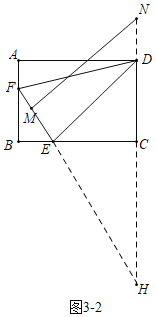
∵y＝x，
解得x＝12，
综上所述，满足条件的CN的值为或12．
练习册系列答案
相关题目
