题目内容
【题目】如图三角形ABC中,AB=3,AC=4,以BC为边向三角形外作等边三角形BCD,连AD,则当∠BAC=_____度时,AD有最大值_____.

【答案】120,7.
【解析】
如图,在直线AC的上方作等边三角形△OAC,连接OD.只要证明△ACB≌△OCD,推出OD=AB=3,推出点D的运动轨迹是以O为圆心OD长为半径的圆,推出当D、O、A共线时,AD的值最大;
解:如图,
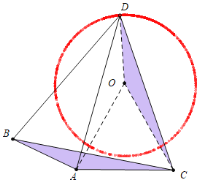
在直线AC的上方作等边三角形△OAC,连接OD.
∵△BCD,△AOC都是等边三角形,
∴CA=CO,CB=CD,∠ACO=∠BCD,
∴∠ACB=∠OCD,
在△ACB和∠OCD中,
 ,
,
∴△ACB≌△OCD,
∴OD=AB=3,
∴点D的运动轨迹是以O为圆心OD长为半径的圆,
∴当D、O、A共线时,AD的值最大,最大值为OA+OD=4+3=7.
∵△ACB≌△OCD,
∴∠CAB=∠DOC,
∵当D、O、A共线时,∠DOC=180°-60°=120°,
∴当∠BAC=120度时,AD有最大值为7.
故答案为120,7.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).