题目内容
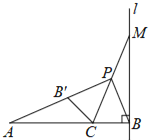
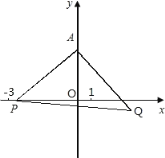
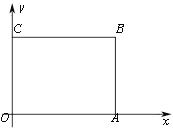
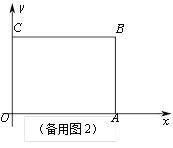
【题目】如图,在直角坐标系中,矩形OABC的边OA在x轴上,OC在y轴上,且B的坐标为(8,6),动点D从B点出发,以1个单位长度每秒的速度向C点运动t秒(D不与B,C重合),连接AD,将△ABD沿AD翻折至△AB'D(B'在矩形的内部或边上),连接DB',DB'所在直线与AC交于点F,与OA所在直线交于点E.
(1)①当t= 秒,B'与F重合;
②求线段CB'的取值范围;
(2)①求EB'的长度(用含t的代数式表示),并求出t的取值范围;
②当t为何值时,△AEF是以AE为底的等腰三角形?并求出此时EC的长度.

【答案】(1)①3;②4≤CB'<8;(2)①EB' =![]() (0<t≤6);②当t为2时,△AEF是以AE为底的等腰三角形,CE=2
(0<t≤6);②当t为2时,△AEF是以AE为底的等腰三角形,CE=2![]() .
.
【解析】
(1)①直接利用题意填写即可;②由题意得,AB=6,然后以点B'的运动轨迹确定CB'的取值范围.(2)①设AE=DE=x,过点D作DM⊥x轴于点M,再应用勾股定理结合题意即可解答;②若△AEF是以AE为底的等腰三角形,则∠AEF=∠EAF,利用全等三角形的相关知识解答即可.
解:(1)①t= 3 秒
②由题意知,AB=AB'=6
所以点B'的运动轨迹为以A为圆心以6为半径的圆
∴CB'的取值范围是 4≤CB'<8
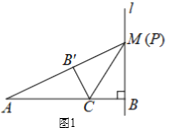
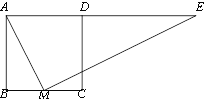
(2)①如图:过点D作DM⊥x轴于点M,易证AE=DE 设AE=DE=x
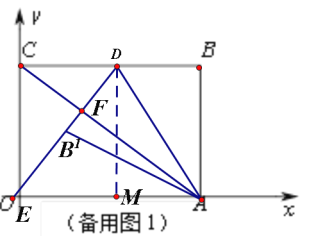
在Rt△DME中 , DM2+ME2=DE2
∴ (x-t)2+62=x2
解得x=![]() +
+![]() .即DE=
.即DE=![]() +
+![]()
∴ EB' =![]() +
+![]() -t
-t
=-![]() +
+![]() (0<t≤6)
(0<t≤6)
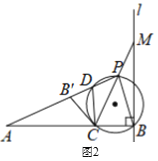
②若△AEF是以AE为底的等腰三角形,则∠AEF=∠EAF
易证△AOC≌△EMD
∴ AC=DE
![]() +
+![]() =10 解得t1=2,t2=18(舍去)
=10 解得t1=2,t2=18(舍去)
当t为2时,△AEF是以AE为底的等腰三角形
此时ME=OA=10,OE=2, CE=2![]() .
.

 智慧小复习系列答案
智慧小复习系列答案