题目内容
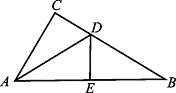
【题目】如图,在直角 ![]() 中,∠C=90°,DC = 2,∠CAB的平分线AD交BC于点D,DE垂直平分AB.求∠B的度数和DB的长.
中,∠C=90°,DC = 2,∠CAB的平分线AD交BC于点D,DE垂直平分AB.求∠B的度数和DB的长.
【答案】∠B=30°,DB=4
【解析】
试题根据DE垂直平分AB,可得∠DAE=∠B,再利用角平分线的性质和三角形内角和定理,即可求得∠B的度数;根据∠CAB的平分线AD交BC于点D,DE⊥AB可知DE=CD=2,在Rt△BDE中根据直角三角形的性质即可得出结论.
试题解析:∵在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,
∴∠DAE=![]() ∠CAB=
∠CAB=![]() (90°-∠B),
(90°-∠B),
∵DE垂直平分AB,
∴AD=BD,
∴∠DAE=∠B,
∴∠DAE=![]() ∠CAB=
∠CAB=![]() (90°-∠B)=∠B,
(90°-∠B)=∠B,
∴3∠B=90°,
∴∠B=30°;
∵在△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,DE⊥AB,
∴DE=CD=2,
∵∠B=30°,
∴BD=2DE=4.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目