题目内容
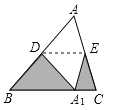
【题目】如图，三角形ABC的面积为1，将三角形ABC沿着过AB的中点D的直线折叠，使点A落在BC边上的
处，折痕为DE，若此时点E是AC的中点，则图中阴影部分的面积为______________．
【答案】
【解析】
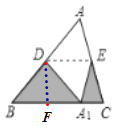
作DF⊥BC于点F. 又D、E分别是AB、AC的中点，DE是三角形的中位线，从而DE∥BC，DE=BC，进而可求S△A1BD+S△A1CE=2 S△A1DE，由折叠得：△ADE≌△A1DE，从而可求得结论．
作DF⊥BC于点F.
∵D、E分别是AB、AC的中点，
∴DE是△ABC的中位线，
∴DE∥BC，DE=BC，
∵S△A1BD+S△A1CE=
=
,
=
,
∴ S△A1BD+S△A1CE=2 S△A1DE,
由折叠得：△ADE≌△A1DE，
∴S△ADE+S△A1DE=S△ABC，
∴S阴影═S△ABC=
，
故答案为：．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
