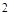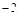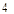题目内容
如图6,直线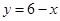 交x轴、y轴于A、B两点,P是反比例函数
交x轴、y轴于A、B两点,P是反比例函数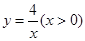 图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F。则
图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F。则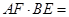

A. 8 B.6 C. 4 D.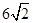
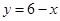 交x轴、y轴于A、B两点,P是反比例函数
交x轴、y轴于A、B两点,P是反比例函数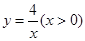 图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F。则
图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F。则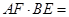

A. 8 B.6 C. 4 D.
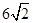
A
分析:首先作辅助线:过点E作EC⊥OB于C,过点F作FD⊥OA于D,然后由直线y=6-x交x轴、y轴于A、B两点,求得点A与B的坐标,则可得OA=OB,即可得△AOB,△BCE,△ADF是等腰直角三角形,则可得AF?BE= 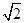 CE?
CE? 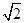 DF=2CE?DF,又由四边形CEPN与MDFP是矩形,可得CE=PN,DF=PM,根据反比例函数的性质即可求得答案.
DF=2CE?DF,又由四边形CEPN与MDFP是矩形,可得CE=PN,DF=PM,根据反比例函数的性质即可求得答案.
解答:解:过点E作EC⊥OB于C,过点F作FD⊥OA于D,
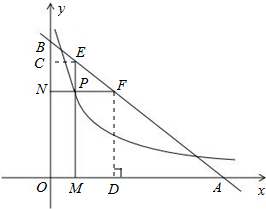
∵直线y=6-x交x轴、y轴于A、B两点,
∴A(6,0),B(0,6),
∴OA=OB,
∴∠ABO=∠BAO=45°,
∴BC=CE,AD=DF,
∵PM⊥OA,PN⊥OB,
∴四边形CEPN与MDFP是矩形,
∴CE=PN,DF=PM,
∵P是反比例函数y=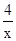 (x>0)图象上的一点,
(x>0)图象上的一点,
∴PN?PM=4,
∴CE?DF=4,
在Rt△BCE中,BE= =
=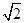 CE,
CE,
在Rt△ADF中,AF= =
=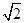 DF,
DF,
∴AF?BE=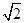 CE?
CE?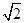 DF=2CE?DF=8.
DF=2CE?DF=8.
故选A.
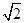 CE?
CE? 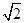 DF=2CE?DF,又由四边形CEPN与MDFP是矩形,可得CE=PN,DF=PM,根据反比例函数的性质即可求得答案.
DF=2CE?DF,又由四边形CEPN与MDFP是矩形,可得CE=PN,DF=PM,根据反比例函数的性质即可求得答案.解答:解:过点E作EC⊥OB于C,过点F作FD⊥OA于D,

∵直线y=6-x交x轴、y轴于A、B两点,
∴A(6,0),B(0,6),
∴OA=OB,
∴∠ABO=∠BAO=45°,
∴BC=CE,AD=DF,
∵PM⊥OA,PN⊥OB,
∴四边形CEPN与MDFP是矩形,
∴CE=PN,DF=PM,
∵P是反比例函数y=
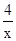 (x>0)图象上的一点,
(x>0)图象上的一点,∴PN?PM=4,
∴CE?DF=4,
在Rt△BCE中,BE=
 =
=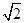 CE,
CE,在Rt△ADF中,AF=
 =
=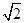 DF,
DF,∴AF?BE=
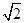 CE?
CE?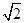 DF=2CE?DF=8.
DF=2CE?DF=8.故选A.

练习册系列答案
相关题目
 轴,垂足为
轴,垂足为 轴交于点F,已知AC:
轴交于点F,已知AC:
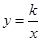 的图象经过点A(1,2).
的图象经过点A(1,2).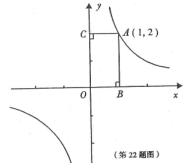
 图象上有三个点
图象上有三个点 ,
, ,
, ,其中
,其中 ,则
,则 ,
, ,
, 的大小关系是__________________
的大小关系是__________________
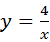 的图象上,则当函数值y≥﹣2时,自变量x的取值范围是 .
的图象上,则当函数值y≥﹣2时,自变量x的取值范围是 .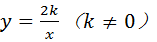 满足:当x<0时,y随x的增大而减小.若该反比例函数的图象与直线
满足:当x<0时,y随x的增大而减小.若该反比例函数的图象与直线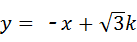 都经过点P,且
都经过点P,且 ,则实数k=___________
,则实数k=___________ 的边长为2,反比例函数
的边长为2,反比例函数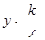 图像过点
图像过点 ,则k的值是
,则k的值是