题目内容
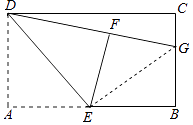
【题目】如图,在矩形ABCD中,E是边AB的中点,连接DE,△ADE沿DE折叠后得到△FDE,点F在矩形ABCD的内部,延长DF交于BC于点G.
(1)求证:FG=BG;
(2)若AB=6,BC=4,求DG的长.
【答案】
(1)
证明:连接EG,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∵△ADE沿DE折叠后得到△FDE,
∴AE=EF,∠DFE=∠A=90°,
∴∠GFE=∠B,
∵E是边AB的中点,
∴AE=BE,
∴EF=EB,
在Rt△EFG与Rt△EBG中, ![]() ,
,
∴Rt△EFG≌Rt△EBG;
∴FG=BG
(2)
解:∵AB=6,BC=4,△ADE沿DE折叠后得到△FDE,
∴DF=DA=4,EF=AE=3,∠AED=∠FED,
∵Rt△EFG≌Rt△EBG,
∴∠FEG=∠BEG,
∴∠DEF+∠FEG=90°,
∵EF⊥DG,
∴EF2=DFFG,
∴FG= ![]() ,
,
∴DG=FG+DF= ![]() .
.
【解析】(1)连接EG,根据矩形的性质得到∠A=∠B=90°,根据折叠的性质得到AE=EF,∠DFE=∠A=90°,根据全等三角形的性质即可得到结论;(2)根据折叠的性质得到DF=DA=4,EF=AE=3,∠AED=∠FED,根据全等三角形的性质得到∠FEG=∠BEG,得到∠DEF+∠FEG=90°,根据射影定理即可得到结论.

练习册系列答案
相关题目