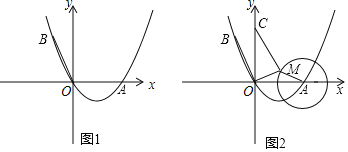Question

【题目】在四边形中，对角线、相交于点，将绕点按逆时针方向旋转得到，旋转角为θ（0°＜θ＜90°），连接、，与交于点．

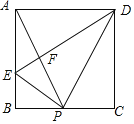
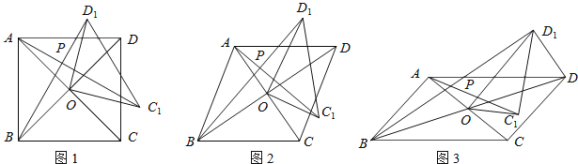
（1）如图1，若四边形是正方形．

①求证：≌．

②请直接写出与的位置关系．

（2）如图2，若四边形是菱形，，，设．判断与的位置关系，说明理由，并求出的值．

（3）如图3，若四边形是平行四边形，，，连接，设．请直接写出的值和的值．

Answer 1

【答案】（1）①证明见解析；②AC1⊥BD1；（2）k=，AC1⊥BD1，理由见解析；（3）k=，AC12+(kDD1)2=25

【解析】

（1）①根据正方形与旋转的性质，通过SAS证明两三角形全等；

②由全等三角形的性质得出，通过证明进行求解；

（2）根据菱形与旋转的性质得出OC1=OA，OD1=OB，∠AOC1=∠BOD1，进而可证明△AOC1∽△BOD1，利用相似三角形的性质进行求解；

（3）同（2）的解法相似可求出k的值，根据旋转的性质得出OD1=OB=OD，进而可得出，利用勾股定理进行求解．

（1）①证明：∵四边形ABCD是正方形，

∴OC=OA=OD=OB，AC⊥BD，

∴∠AOB=∠COD=90°，

∵△COD绕点O按逆时针方向旋转得到△C1OD1，

∴OC1=OC，OD1=OD，∠COC1=∠DOD1，

∴OC1=OD1，∠AOC1=∠BOD1，

在△AOC1和△BOD1中，

，

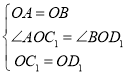∴△AOC1≌△BOD1（SAS）；

②解：AC1⊥BD1，理由如下：

∵△AOC1≌△BOD1，

∴，

∵，

∴，即，

∴AC1⊥BD1；

（2）解：AC1⊥BD1，理由如下：

∵四边形ABCD是菱形，

∴OC=OA=AC，OD=OB=BD，AC⊥BD，

∴∠AOB=∠COD=90°，

∵△COD绕点O按逆时针方向旋转得到△C1OD1，

∴OC1=OC，OD1=OD，∠COC1=∠DOD1，

∴OC1=OA，OD1=OB，∠AOC1=∠BOD1，

∴，

∴△AOC1∽△BOD1，

∴∠OAC1=∠OBD1，

又∵∠AOB=90°，

∴∠OAB+∠ABP+∠OBD1=90°，

∴∠OAB+∠ABP+∠OAC1=90°，

∴∠APB=90°，

∴AC1⊥BD1，

∵△AOC1∽△BOD1，

∴=，

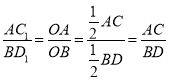∴k=；

（3）解：与（2）一样可证明△AOC1∽△BOD1，

∴，

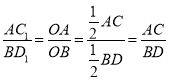
∴k=；

∵△COD绕点O按逆时针方向旋转得到△C1OD1，

∴OD1=OD，而OD=OB，

∴OD1=OB=OD，

∴△BDD1为直角三角形，即，

在Rt△BDD1中，BD12+DD12=BD2=100，

∴(2AC1)2+DD12=100，

∴AC12+(kDD1)2=25．