题目内容
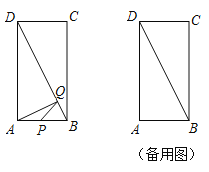
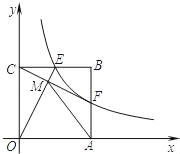
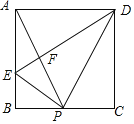
【题目】如图,在矩形ABCD中,P是BC上一点,E是AB上一点,PD平分∠APC,PE⊥PD,连接DE交AP于F,在以下判断中,不正确的是( )
A.当P为BC中点,△APD是等边三角形
B.当△ADE∽△BPE时,P为BC中点
C.当AE=2BE时,AP⊥DE
D.当△APD是等边三角形时,BE+CD=DE
【答案】B
【解析】
A、先判断出△APB≌△DPC,进而可以得出∠APD=60°,即可得出结论;
B、虽然题目中有相似三角形和直角三角形,但没有告诉线段与线段之间的倍数关系和没出现含30°的直角三角形,所以没办法得出点P是BC的中点;
C、先求出∠BAP,进而得出∠ADE=∠PDE,即可判断出△ADE≌△PDE,最后用三角形三线合一的性质即可得出结论;
D、先求出∠BPE=∠APE=∠PAB=30°,再用含30°的直角三角形的性质和勾股定理即可得出结论.
解:A、∵四边形ABCD是矩形,
∴AB=CD,∠B=∠C=90°,
∵点P是BC的中点,
∴PB=PC,
在△APB和△DPC中,
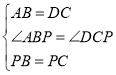 ,
,
∴△APB≌△DPC(SAS),
∴PA=PD,∠APB=∠DPC,
∵PD平分∠APC,
∴∠APD=∠CPD,
∴∠APB=∠APD=∠CPD,
∵∠APB+∠APD+∠CPD=180°,
∴∠APD=60°,
∵PA=PD,
∴△APD是等边三角形;
∴A正确,故A不符合题意;
B、由给出的条件,没办法得出点P是BC的中点,故B符合题意;
C、∵PD⊥PE,
∴∠BPE+∠DPC=90°,∠APE+∠APD=90°,
∵∠APD=∠CPD,
∴∠APE=∠BPE,
过点B作BG∥AP交PE的延长线于G,
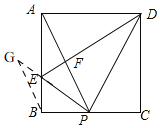
∴∠G=∠APE=∠BPE,
∴BG=BP,
∵BG∥AP,
∴△BEG∽△AEP,
∴![]()
∴![]() ,
,
∵AE=2BE,
∴![]() ,
,
在Rt△ABP中,sin∠BAP=![]() ,
,
∴∠BAP=30°,
∴∠APB=60°,
∴∠BPE=∠APE=30°=∠BAP,
∴AE=PE,
∵EA⊥AD,EP⊥PD,
∴∠ADE=∠PDE,
在△ADE和△PDE中,
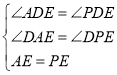 ,
,
∴△ADE≌△PDE,
∴∠AED=∠PED,
∵AE=PE,
∴DE⊥AP,
∴C正确,故C不符合题意;
D、∵△APD是等边三角形,
∴AP=DP,∠APD=60°,
∴∠CPD=60°,
∴∠APB=60°,
∴∠BPE=∠APE=∠PAB=30°
∴AE=PE
设BE=a,
在Rt△PBE中,BP=![]() BE=
BE=![]() a,PE=2a,
a,PE=2a,
∴AE=2a,
∴CD=AB=BE+AE=3a,
易证△APB≌△DPC,
∴PB=PC,
∴AD=BC=2BP=2![]() a,
a,
在Rt△ADE中,根据勾股定理,得,DE=![]() =4a,
=4a,
∵BE+CD=a+3a=4a=DE,
∴D正确,故D不符合题意;
∴符合题意的只有B.
故选:B.

 快乐暑假暑假能力自测中西书局系列答案
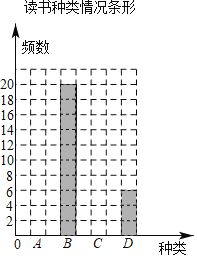
快乐暑假暑假能力自测中西书局系列答案【题目】寒假中,某校七年级开展“阅读经典,读一本好书”的活动.为了解学生阅读情况,从全年级学生中随机抽取了部分学生调查读书种类情况,并进行统计分析,绘制了如下不完整的统计图表:
读书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | a | 32% |
B.文学类 | 20 | 40% |
C.艺术类 | 8 | b |
D.其他类 | 6 | 12% |
请根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)若绘制“阅读情况扇形统计图”,则“艺术类”所对应扇形的圆心角度数为 °;
(3)若该校七年级共有800人,请估计全年级在本次活动中读书种类为“艺术类”的学生人数.