题目内容
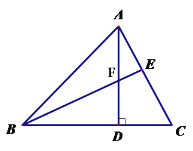
【题目】如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC, FD=CD。求证:(1) Rt△BDF≌Rt△ADC (2) BE⊥AC
【答案】详见解析
【解析】
(1)在Rt△ACD和Rt△BFD中,根据直角边DC=FD和斜边AC=BF对应相等,可证明△BFD≌△ACD;
(2)由△ADC≌△BDF可得BF=AC,因为∠EBC=∠DAC,又因为∠DAC+∠ACD=90°,所以∠EBC+∠ACD=90°,则BE⊥AC.
(1)证明∵∠ADB=∠ADC=90°,
∴在Rt△BDF和Rt△ADC中,
∵BF=AC,DF=DC ,
∴Rt△BDF≌Rt△ADC,
(2)∵Rt△BDF≌Rt△ADC,
∴∠CAD=∠DBF,
∵∠AFE=∠BFD
∴∠CAD+∠AFE=∠DBF+∠BFD=90°,
∴BE⊥AC.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目