题目内容
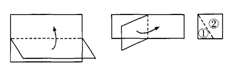
在直线L上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1+S2+S3+S4= 。
 |
4
运用勾股定理可知，每两个相邻的正方形面积和都等于中间斜放的正方形面积，据此即可解答．
解：观察发现，
∵AB=BE，∠ACB=∠BDE=90°，
∴∠ABC+∠BAC=90°，∠ABC+∠EBD=90°，
∴∠BAC=∠BED，
∴△ABC≌△BDE，
S1和S2之间的两个三角形可以证明全等，
则S1+S2即直角三角形的两条直角边的平方和，
根据勾股定理，即S1+S2=1，
同理S3+S4=3．
则S1+S2+S3+S4=1+3=4．
解：观察发现，
∵AB=BE，∠ACB=∠BDE=90°，
∴∠ABC+∠BAC=90°，∠ABC+∠EBD=90°，
∴∠BAC=∠BED，
∴△ABC≌△BDE，
S1和S2之间的两个三角形可以证明全等，
则S1+S2即直角三角形的两条直角边的平方和，
根据勾股定理，即S1+S2=1，
同理S3+S4=3．
则S1+S2+S3+S4=1+3=4．
练习册系列答案
相关题目
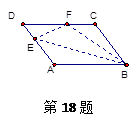
中，
过对角线交点
作
交
于
则
的长是（ ）
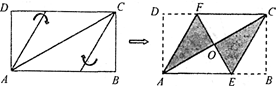
是正方形，点
在
上，
于
，请你在
上确定一点
，使
，并说明理由。