题目内容
【题目】如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( ) 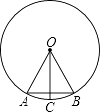
A.△OAB是等边三角形
B.弦AC的长等于圆内接正十二边形的边长
C.OC平分弦AB
D.∠BAC=30°
【答案】D
【解析】解:∵OA=AB=OB, ∴△OAB是等边三角形,选项A正确,
∴∠AOB=60°,
∵OC⊥AB,
∴∠AOC=∠BOC=30°,AC=BC,弧AC=弧BC,
∴ ![]() =12,∠BAC=
=12,∠BAC= ![]() ∠BOC=15°,
∠BOC=15°,
∴选项B、C正确,选项D错误,
故选D.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对正多边形和圆的理解,了解圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目