题目内容
【题目】综合与实践：
发现问题：
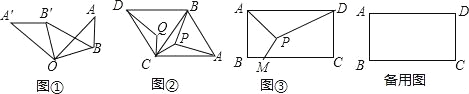
如图①，已知：△OAB中，OB=3，将△OAB绕点O逆时针旋转90°得△OA′B，连接BB′．
则BB′= ．
问题探究：
如图②，已知△ABC是边长为4
的等边三角形，以BC为边向外作等边△BCD，P为△ABC内一点，将线段CP绕点C逆时针旋转60°，P的对应点为Q．
（1）求证：△DCQ≌△BCP
（2）求PA+PB+PC的最小值．
实际应用：
如图③，某货运场为一个矩形场地ABCD，其中AB=500米，AD=800米，顶点A、D为两个出口，现在想在货运广场内建一个货物堆放平台P，在BC边上（含B、C两点）开一个货物入口M，并修建三条专用车道PA、PD、PM．若修建每米专用车道的费用为10000元，当M，P建在何处时，修建专用车道的费用最少？最少费用为多少？
【答案】发现问题：3
；问题探究：（1）证明参见解析；（2）12；实际应用：M建在BC中点（BM=400米）处，点P在过M且垂直于BC的直线上，且在M上方（500﹣
）米处，最少费用为1000000（4
+5）万元．
【解析】
试题分析：发现问题：根据旋转的性质，利用勾股定理直接求得BB'的值；问题探究：（1）由等边三角形的性质和旋转的性质，得到△DCQ≌△BCP的条件；（2）由两点之间线段最短得PA+PB+PC最小时的位置，用等边三角形的性质计算；实际应用：先确定出最小值时的位置，当M，P，P1，D1在同一条直线上时，AP+PM+DP最小，最小值为D1N，再用等边三角形的性质计算．
试题解析：发现问题：由旋转角度可知∠BOB′=90°，OB=OB'=3，根据勾股定理得，BB′=3
；问题探究：（1）∵△BDC是等边三角形，∴CD=CB，∠DCB=60°，由旋转得，∠PCQ=60°，PC=QC，∴∠DCQ=∠BCP，在△DCQ和△BCP中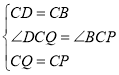
，∴△DCQ≌△BCP；（2）如图1，连接PQ，
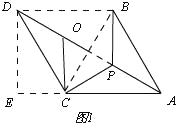∵PC=CQ，∠PCQ=60°∴△CPQ是等边三角形，∴PQ=PC，由（1）有，DQ=PB，∴PA+PB+PC=AP+PQ+QD，由两点之间线段最短得，AP+PQ+QD≥AD，∴PA+PB+PC≥AD，∴当点A，P，Q，D在同一条直线上时，PA+PB+PC取最小值为AD的长，作DE⊥AB，∵△ABC为边长是4
的等边三角形，∴CB=AC=4，∠BCA=60°，∴CD=CB=4，∠DCE=60°，∴DE=6，∠DAE=∠ADC=30°，∴AD=12，即：PA+PB+PC的最小值为12；实际应用：如图2，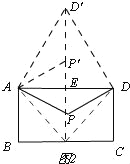
连接AM，DM，将△ADP绕点A逆时针旋转60°，得△AP′D′，由（2）知，当M，P，P′，D′在同一条直线上时，AP+PM+DP最小，最小值为D′M，∵M在BC上，∴当D′M⊥BC时，D′M取最小值，设D′M交AD于E，∵△ADD′是等边三角形，∴EM=AB=500，∴BM=400，PM=EM﹣PE=500﹣
，∴D′E=
AD=400，∴D′M=400+500，∴最少费用为10000×（400+500）=1000000（4+5）万元；∴M建在BC中点（BM=400米）处，点P在过M且垂直于BC的直线上，且在M上方（500﹣
）米处，最少费用为1000000（4+5）万元．
