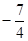题目内容
如图, 抛物线 与
与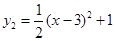 交于点A
交于点A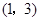 ,过点A作
,过点A作 轴的平行线,分别交两条抛物线于点B、C.
轴的平行线,分别交两条抛物线于点B、C.

则以下结论:①无论 取何值,
取何值, 的值总是正数;②
的值总是正数;② ;
;
③当 时,
时, ;④当
;④当 >
>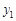 时,0≤
时,0≤ <1;⑤2AB=3AC.其中正确结论的编号是 .
<1;⑤2AB=3AC.其中正确结论的编号是 .
 与
与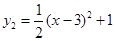 交于点A
交于点A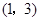 ,过点A作
,过点A作 轴的平行线,分别交两条抛物线于点B、C.
轴的平行线,分别交两条抛物线于点B、C.
则以下结论:①无论
 取何值,
取何值, 的值总是正数;②
的值总是正数;② ;
;③当
 时,
时, ;④当
;④当 >
>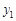 时,0≤
时,0≤ <1;⑤2AB=3AC.其中正确结论的编号是 .
<1;⑤2AB=3AC.其中正确结论的编号是 .①,⑤
试题分析:①∵y2=
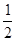 (x-3)2+1﹥0,∴无论x取何值y2的值总是正的;②∵A(1,3)经过y1, ∴3=a(1+2)2-3解得a=
(x-3)2+1﹥0,∴无论x取何值y2的值总是正的;②∵A(1,3)经过y1, ∴3=a(1+2)2-3解得a=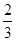 ;③当x=0时,y1=
;③当x=0时,y1=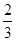 (0+2)2-3=-
(0+2)2-3=- ,y2=
,y2=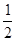 (0-3)2+1=
(0-3)2+1= ∴y2-y1=
∴y2-y1= ④当y2﹥y1时即
④当y2﹥y1时即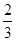 (x+2)2-3﹤
(x+2)2-3﹤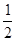 (x-3)2+1.显然0≦x﹤1错误.⑤由二次函数对称性易得;
(x-3)2+1.显然0≦x﹤1错误.⑤由二次函数对称性易得;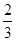 (x+2)2-3=3,x1=1,x2=-5.AB=6,
(x+2)2-3=3,x1=1,x2=-5.AB=6,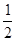 (x-3)2+1=3,x1=1,x2="5" AC=4∴2AB=3AC. ∴只有① ⑤正确。
(x-3)2+1=3,x1=1,x2="5" AC=4∴2AB=3AC. ∴只有① ⑤正确。点评:熟知以上性质,有五问需一一作答,根据已知易求得,有一定的难度,但不大,属于中档题。

练习册系列答案
相关题目
 的图象与
的图象与 轴交于
轴交于 (-1,0)、
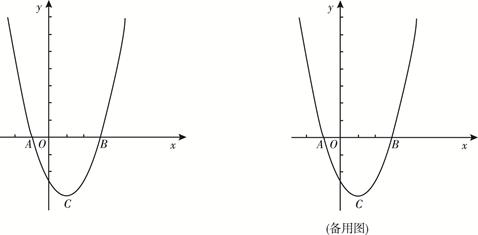
(-1,0)、 (3,0)两点, 顶点为
(3,0)两点, 顶点为 .
.
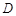 为点
为点 作直线
作直线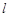 :
: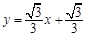 交BD于点E,过点
交BD于点E,过点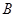 作直线
作直线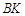 ∥
∥ 交直线
交直线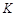 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;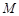 、
、 分别为直线
分别为直线 、
、 、
、 ,求
,求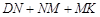 和的最小值.
和的最小值.
 的图象如图所示,根据图象可知:当
的图象如图所示,根据图象可知:当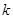 时,方程
时,方程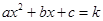 有两个不相等的实数根.
有两个不相等的实数根.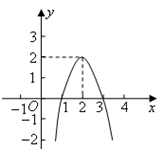
 的一元二次方程
的一元二次方程 有两个实数根
有两个实数根 和
和 .
. 的取值范围;(2)当
的取值范围;(2)当 时,求
时,求 .
.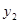 (百元/m²)
(百元/m²) 与x之间满足的函数关系式;请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出
与x之间满足的函数关系式;请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出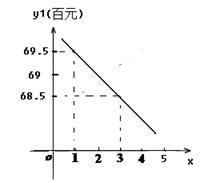
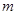 %,楼盘的造价不变,每周的平均销量将比第12周增加5
%,楼盘的造价不变,每周的平均销量将比第12周增加5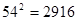 ,
,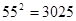 ,
,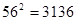 ,
,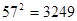 )
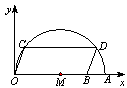
) 
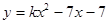 的图象和x轴有交点,则k的取值范围是 ( )
的图象和x轴有交点,则k的取值范围是 ( )