Question

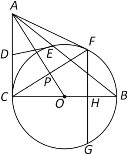
【题目】如图，在边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F，CE⊥AE，垂足为点E，EG⊥CD，垂足为点G，点H在边BC上，BH＝DF，连接AH、FH，FH与AC交于点M．下面结论：①FH＝2BH；②AC⊥FH；③DF＝1；④ EG2＝FGDG．其中正确的个数为（ ）

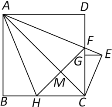
A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

①②证明△ABH≌△ADF，得AF＝AH，再得AC平分∠FAH，则AM既是中线，又是高线，得AC⊥FH，证明BH＝HM＝MF＝FD，则FH＝2BH；所以①②都正确；③证明CM=MF=DF，根据勾股定理即可求解判断；④利用三角函数先得出EG2＝FGCG，再根据中位线得到DG＝CG，所以④也正确．

①②如图1，∵四边形ABCD是正方形，

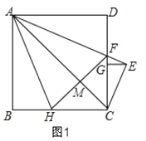
∴AB＝AD，∠B＝∠D＝90°，∠BAD＝90°，

∵AE平分∠DAC，

∴∠FAD＝∠CAF＝22.5°，

∵BH＝DF，

∴△ABH≌△ADF，

∴AH＝AF，∠BAH＝∠FAD＝22.5°，

∴∠HAC＝∠FAC，

∴HM＝FM，AC⊥FH，

∵AE平分∠DAC，

∴DF＝FM，

∴FH＝2DF＝2BH，

故选项①②正确；

③在Rt△FMC中，∠FCM＝45°，

∴△FMC是等腰直角三角形，

∴CM=MF,

∵正方形的边长为2，

∴AC＝2，

∴DF=MF=MC＝AC-AM=AC-AD=22，

所以选项③不正确；

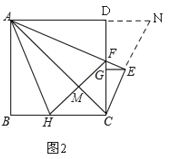
④延长CE和AD交于N，如图2，

∵AE⊥CE，AE平分∠CAD，

∴CE＝EN，

∵EG∥DN，

∴CG＝DG，

在Rt△FEC中，EG⊥FC，

又EF⊥CE

∴∠EFC+∠FCE＝∠GEC+∠FCE =90°

∴∠EFC=∠GEC

∴tan∠EFC=tan∠GEC

故

∴EG2＝FGCG，又CG＝DG

∴EG2＝FGDG，

故选项④正确；

本题正确的结论有3个，

故选：C．