题目内容
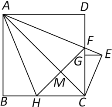
【题目】如图,已知矩形ABCD中,∠ACB=30°,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B′落在AC上,B′C′交AD于点E,在B′C′上取点F,使FB′=AB.
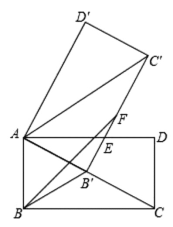
(1)求证:BB′= FB′;
(2)求∠FBB′的度数 ;
(3)已知AB=4,求△BFB′面积.
【答案】(1)详见解析;(2)15°;(3)4
【解析】
(1)关键根据旋转的性质证明△ABB′为等边三角形即可得证;
(2)易知∠B B′F=150°,而BB′= FB′,进而求得∠FBB′的度数;
(3)过B作BH⊥BF交FB′的延长线于H,关键求出BH,利用三角形面积公式即可得解.
证明:(1)∵ 矩形ABCD中,∠ACB=30°
∴∠BAC=60°
由旋转可得:AB′=AB
∴△ABB′为等边三角形,
∴BB′= AB
∵FB′= AB
∴BB′= FB′
(2)解:由(1)得到△ABB′为等边三角形,
∴∠AB′B=60°,
由旋转可得∠AB′F=90°
∴∠BB′F=150°
∴BB′= FB′
∴∠FBB′=∠BFB′=15°;
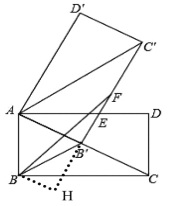
(3)解:过B作BH⊥BF交FB′的延长线于H,
∵∠FBB′=∠BFB′=15°
∴∠B B′H=30°
在Rt△B B′H中,BB′= AB=4, ∠B B′H=30°
∴BH=2
S△BFB′=![]() ,
,

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】水产公司有一种海产品共2104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 | |
售价 | 400 | 300 | 250 | 240 | 200 | 150 | 125 | 120 |
销售量 | 30 | 40 | 48 | 50 | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用反比例函数刻画这种海产品每天的销售量![]() (千克)与销售价格
(千克)与销售价格![]() (元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量
(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量![]() (千克)与销售价格
(千克)与销售价格(元/千克)之间都满足这一关系.
(1)写出这个反比例函数的解析式;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?