Question

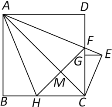
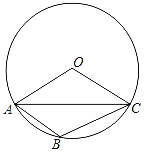
【题目】如图，△ABC内接于⊙O，∠AOC＝∠ABC，AC＝5，则⊙O的半径长为_____．

Answer 1

【答案】．

【解析】

作 所对的圆周角∠APC，作OH⊥AC于H，根据圆周角定理和圆内接四边形的性质可得∠AOC＝120°，则∠OAC＝∠OCA＝30°，再根据垂径定理得到AH＝CH＝AC＝ ，最后根据直角三角形30度所对的边为斜边的一半即可解答．

解：作所对的圆周角∠APC，作OH⊥AC于H，如图，

∵∠APC+∠ABC＝180°，∠AOC＝2∠APC，

∴∠AOC+∠ABC＝180°，

∵∠AOC＝∠ABC，

∴∠AOC+∠AOC＝180°，解得∠AOC＝120°，

∴∠OAC＝∠OCA＝30°，

∵OH⊥AC，

∴AH＝CH＝AC＝，

在Rt△OAH中，OH＝AH＝，

∴OA＝2OH＝，

即⊙O的半径长为．

故答案为．