Question

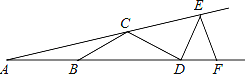
【题目】已知O是AB上的一点，从O点引出射线OC、OE、OD，其中OE平分∠BOC.

（1）如图1，若∠COD是直角，∠DOE=15°，求∠AOE的度数；

（2）如图1，若∠AOC=∠BOD，∠DOE=15°，求∠AOE的度数；

（3）将图1中的∠COD （∠COD仍是直角）绕顶点O顺时针旋转至图2的位置，若∠AOC=, ∠DOE=，请猜想与之间存在什么样的数量关系，写出你的结论，并说明理由.

Answer 1

【答案】（1）105°（2）115°（3）

【解析】

（1）首先求得∠COE的度数，然后根据角平分线的定义求得∠COB的度数，再根据∠AOC=180°-∠BOC，进而得出∠AOE=∠AOC+∠COE即可求解;
②设∠BOE=x,根据角平分线的性质可得∠BOC=2∠BOE=2x,又有∠BOD=∠AOC,得出∠DOE=3x-180°，进而求解;(3) 由∠DOE=,得出∠COE =90°-，然后根据角平分线的定义求得∠BOC,再利用∠AOC+∠BOC=180°即可求解.

（1）∵∠COD是直角，∠DOE=15°

∴∠COE=∠COD-∠DOE=90°-15°=75°,

∵OE平分∠BOC,

∴∠BOC=2∠COE=2×75°=150°,

∴∠AOC=180°-∠BOC=180°-150°=30°,

∴∠AOE=∠AOC+∠COE=30°+75°=105°.

（2）设∠BOE=x,

∵OE平分∠BOC

∴∠BOC=2∠BOE=2x,

∵∠AOC=180°-2x,

∵∠BOD=∠AOC,

∴∠DOE=∠BOE-∠BOD=∠BOE-∠AOC=x-(180°-2x)=3x-180°,

∵∠DOE=15°,

∴3x-180°=15°

∴x=60°,

∴∠AOE=180°-∠BOE=180°-65°=115°;

（3）

理由如下：

∵∠COD是直角，∠DOE=,

∴∠COE=∠COD-∠DOE=90°-,

∵OE平分∠BOC,

∴∠BOC=2∠COE=2(90°-)

∵∠AOC+∠BOC=180°,

∴+2(90°-)=180°,

整理得：.