题目内容
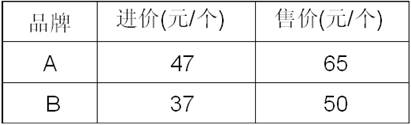
华联超市欲购进A、B两种品牌的书包共400个。已知两种书包的进价和售价如下表所示。设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为w元。
(1)求w关于x的函数关系式;
(2)如果购进两种书包的总费不超过18000元,那么该商场如何进货才能获得最大利润?并求出最大利润。
(提示利润= 售价-进价)

(1)求w关于x的函数关系式;
(2)如果购进两种书包的总费不超过18000元,那么该商场如何进货才能获得最大利润?并求出最大利润。
(提示利润= 售价-进价)
解:(1)∵购进A、B两种品牌的书包共400个,购进A种书包x个,∴购进A种书包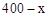 个。
个。
根据题意,得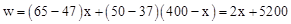 ,
,
∴w关于x的函数关系式为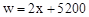 。
。
(2)根据题意,得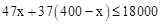 ,
,
解得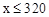 。
。
由(1)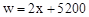 得,w随x的增大而增大,
得,w随x的增大而增大,
∴当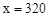 时,w最大,为5840。
时,w最大,为5840。
∴该商场购进A种品牌的书包320个,B两种品牌的书包80个,才能获得最大利润,最大利润为5840元。
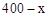 个。
个。根据题意,得
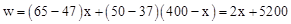 ,
,∴w关于x的函数关系式为
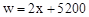 。
。(2)根据题意,得
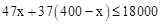 ,
,解得
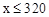 。
。由(1)
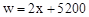 得,w随x的增大而增大,
得,w随x的增大而增大,∴当
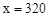 时,w最大,为5840。
时,w最大,为5840。∴该商场购进A种品牌的书包320个,B两种品牌的书包80个,才能获得最大利润,最大利润为5840元。
试题分析:(1)根据利润= 售价-进价列式即可。
(2)根据“购进两种书包的总费不超过18000元”求解,结合一次函数的性质得出结论。

练习册系列答案
相关题目

 的图象经过点(1,-2),则正比例函数的解析式为【 】
的图象经过点(1,-2),则正比例函数的解析式为【 】









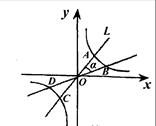
 (n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2012= .
(n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2012= .