题目内容
【题目】有这样一个问题:探究函数![]() 的图象与性质.下面是小文的探究过程,请补充完整:
的图象与性质.下面是小文的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:

如图,在平面直角坐标系![]() 中,描出了以上表中各对应值为坐标的点.
中,描出了以上表中各对应值为坐标的点.
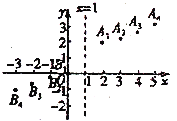
①观察图中各点的位置发现:点![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() 均关于某点中心对称,则该点的坐标为__________;
均关于某点中心对称,则该点的坐标为__________;
②小文分析函数![]() 表达式发现:当
表达式发现:当![]() 时,该函数的最大值为0,则该函数图象在直线
时,该函数的最大值为0,则该函数图象在直线![]() 左侧的最高点的坐标为__________;
左侧的最高点的坐标为__________;
(3)小文补充了该函数图象上两个点![]() ,
,![]() .
.
①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:__________.
【答案】(1)x≠1;(2)①(1,1);②(0,0);(3)①作图见解析;②当x<0时,y随x的增大而增大(答案不唯一).
【解析】
(1)分式的分母不等于零;
(2)①根据中心对称的性质和所对应的点点坐标即可求得,
②根据函数的性质求得即可;
(3)①根据坐标系中的点,用平滑的直线连接即可;
②可以从增减性、渐近性、连续性、与坐标轴交点、图象所在象限等方面作答.
解:(1)依题意得:2x-2≠0,
解得x≠1,
故答案是:x≠1;
(2)①点A1和B1,A2和B2,A3和B3,A4和B4均关于某点中心对称,B1(0,0),A1(2,2),
∴中心点点坐标为(1,1);
②∵当x<1时,该函数的最大值为0,
∴该函数图象在直线x=1左侧的最高点的坐标为(0,0);
故答案为(1,1);(0,0);
(3)①

②该函数的性质:
(ⅰ)当x<0时,y随x的增大而增大;
当0≤x<1时,y随x的增大而减小;
当1<x<2时,y随x的增大而减小;
当x≥2时,y随x的增大而增大.
(ⅱ)函数的图象经过第一、三、四象限.
(ⅲ)函数的图象与直线x=1无交点,图象由两部分组成.
故答案为当x<0时,y随x的增大而增大(答案不唯一);

 科学实验活动册系列答案
科学实验活动册系列答案